Obsah:
- Krok 1:
- Krok 2:
- Krok 3: Fázorový diagram napätia a prúdu pre priebehy
- Krok 4: Fázové uhly prúdu, odporu a napätia sériových obvodov RC
- Krok 5: Impedancia a fázový uhol obvodov radu RC
- Krok 6: Variácia impedancie s frekvenciou
- Krok 7: Variácia impedancie a fázového uhla s frekvenciou
- Krok 8: Ilustrácia toho, ako sa Z a XC menia s frekvenciou
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:55.
- Naposledy zmenené 2025-01-23 15:05.

RC obvody
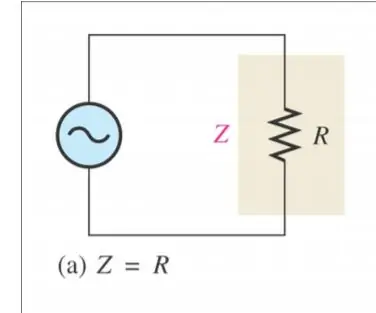
Impedancia: je tým, čo zdroj „vidí“ako úplný odpor voči prúdu
Spôsob výpočtu impedancie sa líši od jedného obvodu
Krok 1:

Keď je obvod čisto kapacitný (obsahuje iba kondenzátor), fázový uhol medzi aplikovaným napätím a celkovým prúdom je 90 ° (prúdové zvody)
Krok 2:

Ak je v obvode kombinácia odporu aj kapacity, fázový uhol medzi odporom (R) a kapacitnou reaktanciou (XC) je 90 ° a fázový uhol pre celkovú impedanciu (Z) je niekde medzi 0 ° a 90 °
Ak je v obvode kombinácia odporu aj kapacity, fázový uhol medzi celkovým prúdom (IT) a napätím kondenzátora (VC) je 90 ° a fázový uhol medzi aplikovaným napätím (VS) a celkovým prúdom (IT) je niekde medzi 0 ° a 90 °, v závislosti od relatívnych hodnôt odporu a kapacity
Krok 3: Fázorový diagram napätia a prúdu pre priebehy

Krok 4: Fázové uhly prúdu, odporu a napätia sériových obvodov RC

Krok 5: Impedancia a fázový uhol obvodov radu RC

- V sériovom obvode RC je celková impedancia fázorovým súčtom R a Xc
- Veľkosť impedancie: Z = √ R^2 + Xc^2 (vektorový súčet)
- Fázový uhol: θ = tan-1 (X C/R)
Prečo používame vektorový súčet, nie algebraický súčet?
Odpoveď: Pretože odpor nezdržiava napätie, ale kondenzátor to robí.
Takže Z = R+Xc je nesprávne.
Aplikácia Ohmovho zákona na celý rad RC obvodov zahŕňa použitie veličín Z, Vs a Itot ako:
Itot = Vs/Z Z = Vs/Itot Vs = Itot * Z
Nezabudnite tiež:
Xc = 1/2πFC
Krok 6: Variácia impedancie s frekvenciou

Krok 7: Variácia impedancie a fázového uhla s frekvenciou

Krok 8: Ilustrácia toho, ako sa Z a XC menia s frekvenciou

R zostáva konštantné
Odporúča:
VYROBTE SI SVOJE OKRUHOVÉ OBVODY ARCÁDOVÝ SÚPRAV FANUÁL HOVORTE IU: 5 krokov

VYROBTE SVOJE OKRUHOVÉ OBVODY ARKÁDOVÝ SÚPRAV FAN HOVORI I <3 U: Teraz môžete svoju arkádovú súpravu snap obvodov nastaviť tak, aby som povedal, že MILUJEM U pomocou tohto návodu! Tiež sa zúčastňujem tohto pokynu v súťaži srdca! Dúfam, že vyhrám
Vytvorte tabuľu pre elektronické obvody - Papercliptronics: 18 krokov (s obrázkami)

Vyrobte si tabuľu pre elektronické obvody-Papercliptronics: Jedná sa o SILNÉ a TRVALÉ elektronické obvody. Aktuálne aktualizácie nájdete na adrese papercliptronics.weebly.com. Vychutnajte si náš podrobný návod na vytváranie domácich elektronických obvodov
Prototypová súprava pre obvody z E-textilu: 5 krokov
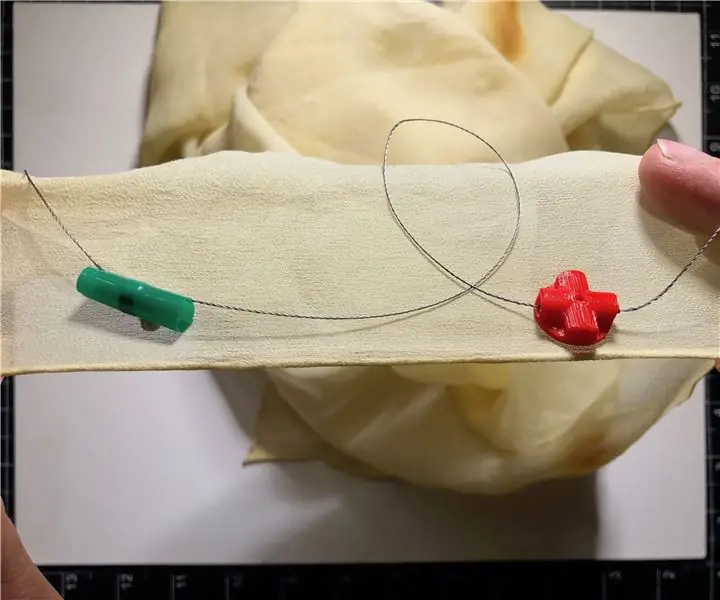
Prototypová súprava pre obvody elektronického textilu: Tento návod vás naučí, ako vytvoriť jednoduchú súpravu na prototypovanie obvodov z elektronického textilu. Táto súprava sa skladá z káblov a spojovacích bodov, ktoré sú opakovane použiteľné, ale robustné. Cieľom tohto projektu je poskytnúť remeselníkom z textilného priemyslu systém, ktorý
Pasívny dolnopriepustný filter pre zvukové obvody (RC filter voľného tvaru): 6 krokov

Pasívny dolnopriepustný filter pre zvukové obvody (RC filter voľného tvaru): Jedna vec, ktorá mi vždy robila problémy pri vytváraní vlastných elektronických nástrojov, je trvalé rušenie mojich zvukových signálov. Skúsil som tienenie a rôzne triky na zapojenie signálov, ale najjednoduchšie riešenie po zostavení sa zdá byť
Zaistite, aby boli integrované obvody SMD priateľské k doske!: 10 krokov (s obrázkami)

Vytvorte priateľské IO k SMD!: Mnohokrát sa stáva, že náš obľúbený integrovaný obvod je k dispozícii iba v balení SMD a neexistuje spôsob, ako ho vyskúšať na doske. V tomto krátkom návode by som vám teda ukázal spôsob, akým som vyrobil tento malý adaptér pre SMD IC tak, aby mohol
