
Obsah:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:57.
- Naposledy zmenené 2025-01-23 15:05.
Podľa arrowlike Nasledovať viac od autora:


V triede často používame stopky na vykonávanie kyvadlového experimentu alebo jednoduchého experimentu s harmonickým pohybom. Tu je výzva, dokážeme vytvoriť skutočný graf jeho pohybu a zistiť, aká je okamžitá uhlová poloha a rýchlosť, to je oveľa viac informácií a zábavy.
Prvá otázka, musíme sa rozhodnúť, že kyvadlovým telesom je beztiažová šnúra alebo tuhá uniformná tyč. Kordový prístup sa zdá byť jednoduchší. Z praxe budovania jedného mám nasledujúce úvahy o kompromise: Najľahším spôsobom zavesenia kyvadlového systému môže byť zavesenie na horný okraj dverí. To vám dáva ~ 2 m dĺžku kyvadla bez akýchkoľvek stavebných stavebných prác. Potrebuje však, aby sa hojdačka nedotkla povrchu dverí, čo celý experiment jednoducho zničí. Rovina, ktorou sa bude kývať, by teda mala byť presne rovnobežná s povrchom vašej steny/dverí. Beztiažová šnúra býva tenká, môže sa ľahko otáčať a komplikovať meranie uhla kyvu. Na meranie stavu švihu chceme použiť jedno meranie. Tenká šnúra, ako napríklad rybárska šnúra, môže byť elastická a roztiahnuteľná, čo ovplyvňuje jednu z našich najdôležitejších konštánt, ktoré sme namerali a použili v rovnici, ktorou je dĺžka kyvadla. Na niektoré môže mať vplyv aj teplota. Závažná hmotnosť visiaca na konci šnúry musí byť dostatočne ťažká, aby sa hmotnosť šnúry stala zanedbateľnou. Vyjadrite sa, ak s nimi súhlasíte alebo nesúhlasíte, alebo máte iné nápady na kompromis v oblasti dizajnu. Na štúdium tohto problému potrebujeme zariadenie, ktoré je také ľahké, že jeho hmotnosť nemožno ignorovať a kyvadlový systém stále považujeme za tuhú rovnomernú tyč. Používam nositeľný elektronický ovládač COTS, ktorý nám prostredníctvom bluetooth pripojenia dodáva informácie o gyroskope, akcelerometri a uhle. Tieto merania budú uložené do dátového súboru aplikácie mobilného telefónu. Potom analyzujeme údaje pre náš jednoduchý experiment s harmonickým pohybom. Numerická analýza sa zameriava na nasledujúce témy: 1) Predpovedajte periódu oscilácie kyvadla 2) Programovateľne zbierajte údaje kyvadlového experimentu s jednoduchými harmonickými pohybmi 3) Na zoskupenie údajov použite kmean a v procese analýzy odstráňte odľahlé hodnoty 4) Na odhad použite krátkodobý FFT frekvencia oscilácie kyvadla
Zásoby
Zariadenie na meranie Bluetooth
Aplikácia pre telefón s Androidom: Choďte do obchodu Google Play, vyhľadajte M2ROBOTS a nainštalujte si ovládaciu aplikáciu. V prípade, že je prístup do obchodu Google Playstore sťažený, navštívte moju osobnú domovskú stránku, kde nájdete alternatívny spôsob sťahovania aplikácií
drevená tyč
niekoľko 3D tlačených dielov
pílové listy alebo podobný kovový materiál
Krok 1: Čo je kyvadlo? Ako to vymodelovať?
Existuje mnoho článkov a kníh, ktoré uvádzajú deriváciu kyvadlovej rovnice, vrátane vašej knihy fyziky učebných osnov. Možno by bolo lepšie, keby sa tu takýto obsah neopakoval. Je tu uvedený iba konečný záver týkajúci sa témy „jednoduchého harmonického pohybu“. Aby sme poznali obdobie kyvadla, potrebujeme vedieť iba dĺžku kyvadla, označovanú ako „l“, v metroch.
Ak sme si celkom istí, že závažie sa nachádza takmer úplne na konci beztiažového lanka visiaceho v čape a kyvadlo sa kýva v malých uhloch θ, povedzme menej ako 15 °, je doba T1 takéhoto kyvadla daná:
T1 = 2*pi*(l/g)^0,5
g = gravitačné zrýchlenie, približne 9,8 m/s^2
Ak je beztiažový kord nahradený tuhou rovnomernou tyčou, opäť s dĺžkou l, jeho jednoduchá harmonická perióda pohybu T2 je daná T1 = 2*pi*(2l/3g)^0,5
V skutočnosti má rovnakú periódu ako beztiažové kordové kyvadlo, čo sú dve tretiny tuhej rovnomernej dĺžky tyče.
Toto je pozadie a môžeme začať pripravovať náš experiment.
Krok 2: Pripravte si diely na stavbu hardvéru



Aby sme vytvorili kyvadlovú štruktúru, 3D diely vytlačíme a zrecyklujeme niečo, čo už máme. Celková štruktúra kyvadla je znázornená na obr.1. Je to zmes dielov 3D tlače spolu s niektorými ručne vyrobenými časťami a dlhým kusom drevenej tyče od Lowe’s.
3D tlačená časť na obr.2 je zavesená na hornom okraji dverí, pretože naše dvere sú pre nás jednoduchým plochým povrchom na zavesenie niečoho. Odkaz na stiahnutie súboru STL:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Zelená časť na obr. 3 spája drevenú tyč s čepeľou a čepeľ sedí na vrchu dvoch kusov koľajníc namontovaných na predchádzajúcom 3D tlačenom závese dverí. Odkaz na stiahnutie súboru STL:
Dva kusy koľajnice sú vyrobené zlomením starého pílového listu na polovicu, pozri obr. 4. Časť na obr. 2 pre ne pripravila správnu veľkosť štrbiny. V ideálnom prípade môžeme pomocou týchto pilníkov v týchto dvoch pílových kotúčoch vytvoriť zárez v tvare „V“. Do zárezov v tvare „V“môže sedieť primerane ostrý kov, ako napríklad britva s jedným ostrím alebo akýkoľvek ručne vyrobený kovový kus. Dôvod, prečo potrebujeme menšiu kontaktnú plochu, je zníženie kinetickej energie stratenej pri švihu.
Posledná 3D vytlačená časť na obr. 5 je malý zásobník na držanie elektronického meracieho zariadenia.
Odkaz na stiahnutie:
Zariadenie na meranie bluetooth generuje odhad uhla, gyroskopické meranie a meranie akcelerometra. Všetky tieto údaje sú nám k dispozícii prostredníctvom bezdrôtového pripojenia bluetooth.
Vykonáme niekoľko experimentov rozmiestnením tohto zariadenia v rôznych polohách ramena kyvadla a uvidíme rozdiely.
Krok 3: Zhromažďovanie údajov z experimentu



Pred analýzou získaného súboru údajov existujú dve uskutočniteľné metódy na zber experimentálnych údajov:
1) Pomocou aplikácie pre telefón s Androidom uvedenej v časti s požiadavkami zaznamenajte všetky merania vytvorené zariadením do dátového súboru uloženého na SD karte vášho telefónu. Môžeme skopírovať súbor a dodatočne spracovať informácie.
2) Pomocou počítača s podporou bluetooth, počítača, prenosného počítača alebo minipočítača RaspberryPi vytvorte bluetooth pripojenie k zariadeniu a prečítajte si údaje na analýzu v reálnom čase alebo offline.
Pre každú metódu existujú klady aj zápory, vyskúšame obe a v tomto návode zistíme rozdiel.
Pri metóde (1) používajúcej aplikáciu pre Android, keď sa nachádzame v ovládacom rozhraní aplikácie pre Android, telemetrické údaje odoslané z meracieho zariadenia bluetooth do telefónu s Androidom budú zaznamenané do súboru denníka s názvom m2flightDatayyyymmdd_hhmmss.txt. Nájdete ho v priečinku Download/m2LogFiles vášho telefónu s Androidom. Priečinok „Stiahnuť“je už existujúcim priečinkom v systéme Android vášho telefónu a „m2LogFiles“je priečinok, ktorý aplikácia vytvorila. Obsah názvu súboru rrrrmmdd_hhmmss je spôsob, ako zakódovať čas začiatku experimentu (rok, mesiac, deň, hodina, minúta a s) v názve súboru.
Každý riadok v súbore denníka je jeden záznam. Začína sa časovou pečiatkou udalosti, preambulovým reťazcom „eam:“, za ktorým nasledujú 4 tripletové údaje, ktorými sú:
Čítanie osi XYZ akcelerometra v hodnotách spätného čítania surového hardvérového senzora
Čítanie osi XYZ gyroskopu v hodnotách spätného čítania surového hardvérového senzora
Čítanie osi XYZ magnetometra v hodnotách spätného čítania surového hardvérového senzora
palubný odhadovaný roll/pitch/raw v stupňoch
Dátový súbor vytvorený pomocou počítačového programu python bude používať identický formát dátových súborov, takže program, ktorý používame v kroku analýzy údajov, nebude obťažovaný zdrojom údajov, ktorý vytvára náš program python alebo aplikácia pre Android.
Začneme kódovať pomocou metódy (2).
Na interakciu s prístrojom na meranie bluetooth sú k dispozícii dve varianty SDK:
1) Python SDK, ktorý je možné nainštalovať pomocou „pip3 install m2controller“, je použitý jazyk python3. Príklady kódu užívateľskej aplikácie sú uložené na adrese https://github.com/xiapeiqing/m2robots/tree/maste…. Na tento experiment použijeme skript python pendulum1.py
2) Java SDK, ktorá sa v tomto návode nepoužíva, pretože chceme neskoršiu vizualizáciu a analýzu získaných údajov kyvadla, čo môže pri programovaní v Jave vyžadovať trochu viac úsilia.
Zdrojový kód programu na zber údajov python3 obsahuje mnoho komentárov k podrobnostiam o funkcii kódu. Tu nájdete snímku zdrojového kódu.
#!/usr/bin/env python#-*-kódovanie: UTF-8-*-z m2controller import m2controller z m2controller import m2Const import signálu import čas import datetime import usrCfg import pendulum2
requestExit = False
################################################################
#chceme používať rovnakú konvenciu pomenovania súborov denníka, aby modul analýzy údajov pendulum2.py mohol byť agnostický pre to, ako získame súbor s údajmi denníka #################### ##################################################### logfilename = " m2flightData%s.txt "%(datetime.datetime.fromtimestamp (time.time ()). strftime ('%Y%m%d_%H%M%S')) dataLogfile = open (logfilename," w ")
def signal_handler (sig, rámec):
global requestExit print ('užívateľ Ctrl-C na ukončenie vykonávania programu') requestExit = True signal.signal (signal. SIGINT, signal_handler)
################################################################
#keď budú k dispozícii všetky údaje o meraní pri frekvencii 20 Hz, bude vyvolaná táto funkcia „spätného volania“################################## ##################################### def callbackfunc (telemetry): strTimeStamp = datetime.datetime.fromtimestamp (time.time ()). strftime ('%H:%M:%S.%f') [:-3] dataStr = "%s, eam:%d,%d,%d,%d,%d,%d, %d, %d, %d, %2.1f, %2.1f, %2.1f / n " %(strTimeStamp, telemetry ['m_fAccelHwUnit'] [0], telemetria ['m_fAccelHwUnit'] [1], telemetria ['m_fAccelHwUnit'] [2], telemetria ['m_fGyroHwUnit'] [0], telemetria ['m_fGyroHwUnit'] [1], telemetria ['m_fGyroHwUnit'] [2], telemetria ['m_fMagHwUemet'] ['m_fMagHwUnit'] [1], telemetria ['m_fMagHwUnit'] [2], telemetria ['m_fRPYdeg'] [0], telemetria ['m_fRPYdeg'] [1], telemetria ['m_fRPYdeg'] [2]) ## ####################################################################################################################################################################### ###############vytlačíme dátový reťazec na obrazovku a uložíme ho do súboru denníka ######################### ################################################# print (dataStr) dataLogfile.writelines (dataStr)
################################################################
#inicializujte ovládač, nezabudnite nastaviť pole BleMACaddress na MAC adresu vášho zariadenia ##################################### ####################################TODO: inicializujme adresu BleMAC, ak ju nenastavuje používateľ. controller = m2controller. BleCtrller (m2Const.etDebian, callbackfunc, usrCfg. BleMACaddress) controller.connect () while True: ############################### #############################################počkajte, kým sa údaje o meraní vytvoria a odošlú z kyvadlového merania prístroj ########################################################################### ################ controller.m_CommsTunnel.waitForNotifications (1.0) if requestExit: ############################ ################################################ udržiavanie domu tu, keď dokončíme zaznamenávanie údajov ######################################################################################################################################################################### ############### controller.stop () dataLogfile.close () break
################################################################
#Zhromažďovanie údajov bolo dokončené, teraz analyzujeme údaje denníka ############################################# ############################ pendulum2.parseDataLogFile (logfilename)
Ak chcete získať dlhodobú aktualizáciu, navštívte stránku
Teraz si vysvetlíme spôsob jeho fungovania. Tento program python je napísaný na vrchu balíka, ktorý je možné nainštalovať pomocou pipu, s názvom m2controller. Balíček nižšej úrovne ponúka mechanizmus spätného volania, takže každá aktualizácia prijatého merania spustí funkciu spätného volania, ktorú sme napísali, a uloží údaje do lokálneho súboru denníka. Formát dátového obsahu súboru denníka je zhodný s formátom, ktorý vytvára sprievodná aplikácia pre Android, takže súbor denníka údajov vytvorený programom python alebo sprievodnou aplikáciou andriod je možné zameniť.
Používateľský signál ctrl-C zachytený operačným systémom je odoslaný do programu a zastaví nekonečnú slučku čakajúcu na nový príchod nameraných údajov.
Doteraz bol súbor denníka úspešne vytvorený a tento program zavolá program na analýzu výsledkov našich experimentov.
Tu sú dva experimenty a porovnanie ukazuje veľmi citeľný rozdiel po pripojení 7gramového zariadenia na rôzne miesta.
Na obrázku 2 používame váhu na určenie skutočnej hmotnosti tohto bluetooth meracieho zariadenia.
Obr. 3 zobrazuje nastavenie kyvadla, kde je 7 gramové zariadenie pripevnené k dolnému koncu kyvadla. Konfigurácia nastavenia na obr. 4 má hmotnosť 7 gramov umiestnenú oveľa bližšie k výkyvnému čapu.
Obr. 5 je detailný pohľad na kyvadlovú štruktúru.
Krok 4: Analýza údajov



Bluetooth merací prístroj váži ~ 7 gramov, čo váži oveľa menej ako ~ 1,6 metra dlhú drevenú palicu. Použite predpoklad „tuhej rovnomernej tyče“a máme túto rovnicu kyvadlového obdobia, T1 = 2*pi*(2l/3g)^0,5
Na získanie gravitačnej konštanty môžeme použiť 9,8 m/s^2. Ale presnejšiu gravitačnú konštantu v akejkoľvek danej geolokácii je možné získať z tejto webovej služby:
www.wolframalpha.com/widgets/view.jsp?id=e…
Pre san francisco je to 9,81278 m/s^2
Dĺžka kyvadla sa meria na 64,5"
2*pi*sqrt (2*64,5*0,0254/(3*9,81278)) poskytuje očakávanú dobu kyvadla 2,0962 (s).
Uvidíme, či to bude v súlade s našimi experimentmi.
V 1. experimente má nastavenie kyvadla 7gramové zariadenie pripevnené k dolnému koncu kyvadla. Môj súbor denníka je možné stiahnuť v:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Premenujte ho na „PendulumTestData.txt“a vložte ho do rovnakého priečinka programu na analýzu pythonu. Tu nájdete snímku zdrojového kódu.
#!/usr/bin/env python#-*-kódovanie: UTF-8-*-import csv import matplotlib.pyplot ako plt plt.style.use ('seaborn-whitegrid') import numpy as np from datetime import datetime, timedelta import seaborn ako sns zo sklearn.cluster import KMeans from collections import Counter ###################################### ###################################táto funkcia spustí prácu s dátovými súbormi ############### ####################################################################################################################################################################### ## def parseDataLogFile (názov súboru údajov): ################################################ ##########################extrahujte údaje do súboru denníkov oddelených čiarkami (CSV) a uložte obsah v každom stĺpci do jednej premennej typu float ## ####################################################################################################################################################################### ############# s otvoreným (názov súboru údajov) ako súbor csv: readCSV = csv.reader (csvfile, delimiter = ',') timestampS = fAccelHwUnit_x = fAccelHwUnit_y = fAccelHwUnit_z = fGyroHwUnit_x = fGyroHwUnit_y = fGyroHwUnit_z = fMagHwUnit_x = fMagHwUnit_y = fMagHwUni t_z = fRPYdeg_r = fRPYdeg_p = fRPYdeg_y = pre riadok v readCSV: skúste: x = datetime.strptime (riadok [0].split (',') [0], '%H:%M:%S.%f ') timestampS.append (timedelta (hodiny = x.hodina, minúty = x.minúta, sekundy = x.sekunda, mikrosekundy = x mikrosekunda).total_seconds ()) fAccelHwUnit_x.append (float (riadok) [1] [4:])) fAccelHwUnit_y.append (float (riadok [2])) fAccelHwUnit_z.append (float (riadok [3])) fGyroHwUnit_x.append (float (riadok [4])) fGyroHwUnit_y.append (float (riadok [5]) fGyroHwUnit_z.append (float (riadok [6])) fMagHwUnit_x.append (float (riadok [7])) fMagHwUnit_y.append (float (riadok [8])) fMagHwUnit_z.append (float (riadok) [9])) fRPYdeg_r.append (float (riadok [10])) fRPYdeg_p.append (float (riadok [11])) fRPYdeg_y.append (float (riadok [12])) okrem: prejsť timestampS = np.asarray (časové pečiatky) časové značky = časové značky - časové pečiatky [0] = fAccelHwUnit_x np.asarray (fAccelHwUnit_x) fAccelHwUnit_y = np.asarray (fAccelHwUnit_y) fAccelHwUnit_z = np.asarray (fAccelHwUnit_z) fGyroHwUnit_x = np.asarray (fGyroHwUnit_x) fGyroHwUnit_y = np.asarray (fGyroHwUnit_y) fGyroH wUnit_z = np.asarray (fGyroHwUnit_z) fMagHwUnit_x = np.asarray (fMagHwUnit_x) fMagHwUnit_y = np.asarray (fMagHwUnit_y) fMagHwUnit_z = np.asarray (fMagHwUnit_z) fRPYdeg_r = np.asarray (fRPYdeg_r) fRPYdeg_p = np.asarray (fRPYdeg_p) fRPYdeg_p = fRPYdeg_p - np.mean (fRPYdeg_p) fRPYdeg_y = np.asarray (fRPYdeg_y)
################################################################
#na presný odhad obdobia oscilácie potrebujeme presný odhad vzorkovacej frekvencie ####################################### ################################ FsHz = getSamplingIntervalS (timestampS) ################### ########################################################################### ## výškový komponent vo výstupe referenčného systému polohy smeru nadpisu pre analýzu obdobia kyvadla ########################################## ############################## analyze_timeSequence (timestampS, fRPYdeg_p, FsHz, 'pitch') ############# ####################################################################################################################################################################### ####použite akceleromterový surový výstup merania na analýzu kyvadlového obdobia ########################################################## ############################### analyze_timeSequence (timestampS, fAccelHwUnit_x, FsHz, 'accel') ############# ####################################################################################################################################################################### ####použite gyroskopický surový výstup merania na analýzu kyvadlového obdobia ########################################################## ############################## analyze_timeSequence (timestampS, fGyroHwUnit_y, FsHz, ' gyro ') tlač (' hotovo, gratulujem:-) ') plt.show () ################################### #########################################v procese bluetooth komunikácie, existuje zriedkavá šanca, že by dátový komunikačný paket mohol byť stratený#používame K-mean na izoláciu 20Hz údajov o meraní od extrémnych hodnôt, ktoré sú spôsobené vypadnutím paketu#ponor do „signálu a systému pre ďalšie podrobnosti“################### ########################################################################################################################################################################################################## (timestampS): plt.figure () sampleIntervalS = np.diff (timestampS) sns.distplot (sampleIntervalS) plt.ylabel ('histogram') plt.xlabel ('measurement interval (s)') clusterCnt = 5 km = KMeans (n_clusters = clusterCnt) km.fit (sampleIntervalS.reshape (-1, 1)) centroidy = km.cluster_centers_ elemCnt = Počítadlo (km.labels_) výskytCnt = pre ii v dosahu (clusterCnt):]) FsHz = 1/centroidy [výskytCnt.index (max (výskytCnt))] návrat FsHz
################################################################
#použite spektrometer, tj. krátky čas FFT na získanie frekvenčnej zložky, vrchol píkov je náš najlepší odhad kyvadlovej oscilácie ############################# ################################################# analyze_timeSequence (timestampS, timeSeqData, FsHz, strComment): fig, (ax1, ax2) = pl.subplots (nrows = 2) ax1.plot (timestampS, timeSeqData, marker = 'o', markerfacecolor = 'blue', markersize = 2, color = 'skyblue', linewidth = 1) ax1.set_title ("meranie časovej oblasti kyvadla - %s" %strComment) ax1.set_xlabel ("čas vzorkovania (druhý)") ax1.set_ylabel (strComment); NFFT = 2048 # dĺžka segmentov okna
Pxx, freqs, bins, im = ax2.specgram (timeSeqData, NFFT = NFFT, Fs = FsHz, noverlap = NFFT/2)
ax2.set_title ("Spectrogram") ax2.set_xlabel ("vzorky") ax2.set_ylabel ("frekvencia (Hz)");
# Metóda `specgram 'vráti 4 objekty. Oni sú:
# - Pxx: periodogram # - frekvencie: vektor frekvencie # - zásobníky: stredy časových zásobníkov # - im: inštancia matplotlib.image. AxesImage predstavujúca údaje v grafe pkresult = np.where (Pxx == np.amax (Pxx)) oscFreqHz = freqs [pkresult [0] [0] print ('oscilácia kyvadla Freq (Hz) =%f, Perioda (Sec) =%f, odhad dátového zdroja:%s'%(oscFreqHz, 1/oscFreqHz, strComment)) návrat 1/oscFreqHz
################################################################
#máme tento program spustiť nezávisle, tj. bez toho, aby ho volal pendulum1.py,#definujeme predvolený názov súboru s údajmi denníka, ktorý sa má analyzovať ###################### ################################################### if _name_ == "_main_ ": defaultFilename = './PendulumTestData.txt' import os.path if os.path.isfile (defaultFilename): parseDataLogFile (defaultFilename) else: print (" default log file %s not existing " %defaultFilename)
Ak chcete získať dlhodobú aktualizáciu, navštívte stránku
Zdrojový kód obsahuje podrobné komentáre, poskytnime tu súhrn matematického odhadu na vysokej úrovni.
1) Najprv načítame obsah súboru CSV do počítača pomocou balíka python s názvom „csv“. Máme pravidelné meranie.
21: 34: 26,362, lúč: 0, -128, 14464, -8, 144, -96, 2112, -1280, 1664, -0,5, -5,5, 40,5
21: 34: 26,373, lúč: 128, 0, 14272, -8, 136, 40, 2112, -1280, 1664, -0,5, -6,5, 40,0
21: 34: 26,412, lúč: 448, -64, 14208, -8, 136, 24, 2176, -1280, 1664, -0,5, -7,5, 40,5
21: 34: 26,462, lúč: 448, -128, 14272, -8, 120, 16, 2176, -1280, 1664, -0,5, -8,0, 40,5
2) Pretože je rýchlosť merania taká kritická a priamo zavádza chybu odhadu periódy, chceme ich odhadnúť. Náš nominálny interval merania je 50 ms, t.j. 20 Hz. Priemer za všetky merania sa zdá byť v poriadku, ale príležitostne stratíme paket na prenos údajov, interval aktualizácie je 100 ms alebo 150 ms, …
Ak vykreslíme výskyt týchto údajov, pozri obr. 1, ako človek, môžeme mať ľahko očnú hodnotu 0,05 s. Môžeme to však urobiť lepšie?
Na to, aby sme vybrali priemerné výpočty, musíme použiť iba klasifikačnú metódu. Python má súbor nástrojov s názvom KMeans, ktorý nám pomáha s klastrovaním alebo povedzme klasifikáciou. Tieto koncepty sa používajú v mnohých oblastiach veľkých dát a AI.
3) Obr.2 obsahuje dva obrázky. Horný graf je sekvencia časovej domény nášho merania uhla kývania v stupňoch. S odkazom na časovú pečiatku osi x v sekunde môžeme prečítať približne 22,5 cyklov za 50 sekúnd, čo v preklade znamená 2,22 s periódu kyvadla. Existuje spôsob, ako automatizovať tento proces a získať presnejší odhad? Áno, môžeme použiť matematický nástroj nazývaný spektrogram, ktorý používa malý kúsok nameraných údajov a hovorí nám o jeho frekvencii, pozri obrázok nižšie. Čítanie osi y pre najtmavšiu čiaru je frekvencia oscilácie kyvadla. Horizontálna čiara potvrdzuje, že oscilácia kyvadla sa počas experimentu vôbec nezmenila. Inverzná hodnota frekvencie kmitov je perióda oscilácie kyvadla.
Záverečná správa programu je textové zhrnutie:
oscilácia kyvadla Freq (Hz) = 0,449224, perióda (s) = 2,226059, zdroj údajov odhadu: výška tónu
Môžeme zistiť, že náš predchádzajúci výsledok výpočtu očnej bulvy, 2,22 s, je celkom v súlade s vypočítanou hodnotou programu.
V porovnaní s teoreticky vypočítanou hodnotou 2,0962 (s) máme zostávajúcu chybu ~ 5%. Ako sa ich zbaviť? Pamätáte si predpoklad, že je „tuhá uniformná tyč“? Aj 7 gramov hmotnosti navyše sa zdá byť triviálne, je to najväčšia príčina zostávajúcej chyby.
Teraz presunieme zariadenie v blízkosti čapu. Podrobnú fotografiu nájdete v predchádzajúcom kroku. Protokol, ktorý som vytvoril, je možné stiahnuť tu:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Vykonajte rovnaké analytické kroky a získame periódu 2,089867 (s), pozri obr. 3, ktorá je takmer identická s teoretickou predikciou. Skvelé!
Pretože nemáme len meranie uhla kyvu, ale aj gyroskopické meranie a meranie akcelerometrom rovnakou rýchlosťou. Vykonajte rovnakú analýzu pre ďalšie dve merania, výsledky získame na obr. 4 a 5. Odhady zo všetkých troch zdrojov merania súhlasia, čo nás presvedčí o úspechu nášho experimentu.
Tu je výsledok ako konečný výstup spusteného programu python:
oscilácia kyvadla Freq (Hz) = 0,478499, perióda (s) = 2,089867, zdroj údajov odhadu: výška tónu
oscilácia kyvadla Freq (Hz) = 0,478499, perióda (s) = 2,089867, zdroj údajov odhadu: accel
oscilácia kyvadla Freq (Hz) = 0,478499, perióda (s) = 2,089867, zdroj údajov odhadu: gyroskop
Posledná úvaha v tomto kroku, ako môžu byť výsledky odhadov úplne identické pri použití iného zdroja vstupných údajov? Je to protiintuitívna. Túto otázku nechám na čitateľov. Tu je tip: pamätáte si, že používame krátkodobý FFT na odhad frekvencie oscilácií? V digitálnej doméne je odhad frekvencie uvedený v diskrétnych frekvenčných zásobníkoch namiesto odhadu s pohyblivým počtom.
Krok 5: Odporúčania pre budúcu prácu
Existuje niekoľko kategórií odporúčaní pre budúcu prácu.
V predchádzajúcom kroku sa nám podarilo znížiť chybu experimentu z ~ 5% na menej ako 1%, dokážeme to lepšie? Všimnite si, že veľkosť oscilácie klesá exponenciálne, jedným z prispievajúcich faktorov môže byť odpor vzduchu spôsobený pri kývaní kyvadla. Možno bude potrebné upraviť prierez kyvadla tak, aby mal aerodynamický tvar, aby sa znížil aerodynamický odpor.
Môžeme na získanie konštantného signálu špičkovej veľkosti použiť časovo premenlivý zisk naučený pomocou techník adaptívneho filtra. Medzitým korelujte s útlmom veľkosti a vonkajšími silami.
Sotva nájdeme niečo jednoduchšie ako „jednoduchý harmonický pohyb“. Môžeme použiť zariadenia, ktoré analyzujeme kyvadlo, na analýzu niečoho komplikovanejšieho, športovej aktivity, sekvencie štartu vodnej rakety atď.?
Veselé hackovanie
Odporúča:
Simulačná štúdia: 9 krokov
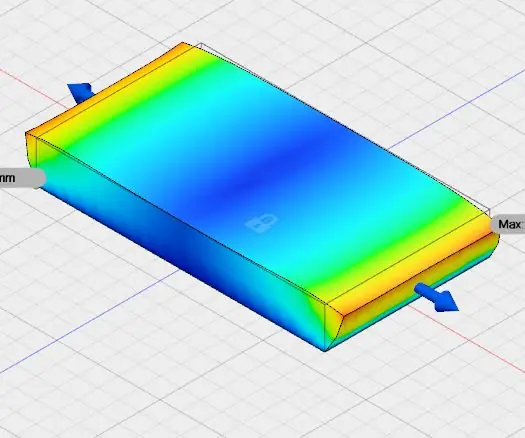
Simulačná štúdia: V tomto návode som použil fusion 360 spoločnosti Autodesk. Tento návod je určený pre simulačnú štúdiu. V tomto som použil modelový a simulačný pracovný priestor auto desk fusion 360. Študoval som simuláciu pre pozdĺžne sily s veľkosťou 10 N. V
Vylepšite svojpomocný zavlažovací hrniec pomocou WiFi na kutilský detektor pohybu s detekciou pohybu a sadbovačom: 17 krokov

Vylepšite svojpomocný zavlažovací kvetináč pomocou WiFi na kutilský detektor pohybu detektora pohybu : V tomto článku vám ukážeme, ako upgradovať svoj vlastný zavlažovací kvetináč s WiFi na samonavlažovací kvetináč s WiFi a alarmom detekcie pohybu. nečítali ste článok o tom, ako si postaviť svojpomocný zavlažovací hrniec pomocou WiFi, môžete
Štúdia prachu Arduino: 8 krokov

Štúdia prachu Arduino: Aké by to bolo žiť na Marse? Je vzduch priedušný? Je to bezpečné? Koľko je tam prachu? Ako často sú búrky? Zaujímala vás niekedy odpoveď na niektorú z týchto otázok?
Vybudovanie domáceho štúdia s veľkým rozpočtom: 8 krokov (s obrázkami)

Vybudovanie domáceho štúdia s veľkým rozpočtom: Keďže nám digitálny vek stále ukazuje, ako technológie znížili potrebu profesionálnych služieb, je stále jednoduchšie dosiahnuť dobré výsledky v umeleckých formách, ako je napríklad zvukový záznam. Mojím cieľom je predviesť nákladovo najefektívnejší spôsob
Skutočne lacné nahrávanie bez úplného štúdia: 5 krokov

Skutočne lacné nahrávanie bez úplného štúdia: v tomto návode vám ukážem, ako nahrávať veci z vašej gitary vo vynikajúcej kvalite, bez štúdia a skutočne lacno. Toto je môj prvý návod, takže si veľmi vážim všetky návrhy, ako to zlepšiť. ini
