Eyeballing Predpis vašej očnej bulvy: projekt BME60B: 9 krokov

2024 Autor: John Day | [email protected]. Naposledy zmenené: 2024-01-30 11:55

Autor: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Zväčšenie je jednou z kľúčových vlastností okuliarov na čítanie, ktoré sú klasifikované podľa predpisu dioptrií. Podľa Michiganskej technologickej univerzity je dioptria ohniskovou vzdialenosťou šošovky, ktorá sa zvyčajne meria v mm, v jednotkách metrov (Michiganská technologická univerzita). Pretože okuliare na čítanie majú konvexné šošovky, ohnisková vzdialenosť by bola kladná, čo by spôsobilo, že by boli pozitívne aj dioptrie (HyperPhysics). Ohnisková vzdialenosť sa zvyšuje so vzdialenosťou medzi objektom ďalej od skutočnej šošovky, čo vedie k zníženiu dioptrií, pretože sú nepriamo úmerné. Preto by okuliare na čítanie s ďalšími dioptriami pomohli objektívu priblížiť zobrazenie tak, aby sa zdalo, že ohnisková vzdialenosť je nižšia, zvýšením hodnoty dioptrií.

Predložený kód bude použitý na predikciu dioptrie šošovky s neznámym predpisom. Na výpočet predpisu sa používajú dva vstupy: fotografia kontrolovaného pozadia bez použitia akýchkoľvek šošoviek a ďalšia fotografia rovnakého pozadia, ale prostredníctvom zvoleného objektívu. Program zmeria skreslenie medzi týmito dvoma fotografiami. Odtiaľ budeme schopní odhadnúť dioptrie objektívu a vygenerovať výsledok, ktorý si používateľ bude môcť pozrieť.

Na tento návod budete potrebovať:

• Čiernobiely šachovnicový vzor vytlačený na liste papiera 11x8,5
• Fotoaparát so schopnosťou zablokovať zaostrenie
• Statív alebo niečo podobné na zaistenie fotoaparátu
• Rôzne recepty na okuliare na čítanie
• MATLAB

Krok 1: Fotografujte

Aby ste mohli vypočítať zväčšenie šošovky, musíte ju vedieť porovnať so skutočnou veľkosťou objektu. V tomto projekte budeme porovnávať zväčšený obrázok s kontrolným obrázkom.

Prvým krokom je teda nasnímanie dvoch fotografií rovnakého obrázku - prvý iba fotoaparátom a druhý objektívom okuliarov na čítanie, ktoré chcete testovať.

Odfotíte čiernobielu šachovnicu s rozmermi 8,5 x 11 palcov a mriežkou 1 palcov. Nastavte fotoaparát 11 palcov od šachovnice. Pred fotografovaním uzamknite zaostrenie na šachovnici.

Odfoťte šachovnicu bez okuliarov na čítanie. Potom bez toho, aby ste s čímkoľvek pohli, položte okuliare na čítanie pred fotoaparát a urobte druhú fotografiu.

Dbajte na to, aby sa poloha fotoaparátu medzi zábermi nepohybovala. Jediné, čo by sa medzi týmito dvoma fotografiami malo zmeniť, je prítomnosť šošovky okuliarov pred fotoaparátom.

Keď skončíte s fotografiami, nahrajte ich do počítača.

Krok 2: Načítajte obrázky do programu MATLAB

Otvorte nový skript.

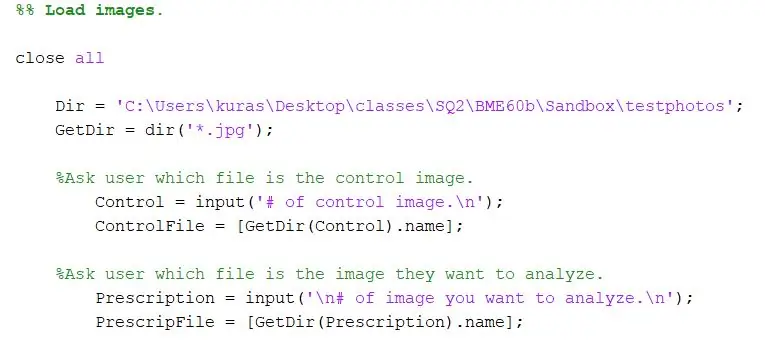
Najprv zadajte adresár, kde sú fotografie uložené. Potom pomocou funkcie dir extrahujte obrázky vo formáte-j.webp

Dir = 'C: / Users / kuras / Desktop / classes / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

V prípade nášho projektu sme chceli užívateľa programu vyzvať, aby hľadal porovnanie súborov. Prvá časť požaduje, aby používateľ zadal kontrolný obrázok, a druhá požaduje, aby používateľ zadal testovací obrázok.

• %Opýtajte sa používateľa, ktorý súbor je kontrolným obrázkom.
• Control = vstup ('# riadiaceho obrázku. / N');
• ControlFile = [GetDir (Control).name]
• %Opýtajte sa používateľa, ktorý súbor je obrázok, ktorý chce analyzovať.
• ChooseFile = vstup ('\ n# obrázku, ktorý chcete analyzovať. / N');
• PrescripFile = [GetDir (ChooseFile).name];

Krok 3: Analýza obrazu

Farebný obrázok v MATLABe má veľkosť MxNx3, zatiaľ čo obrázok v odtieňoch sivej je MxN. To znamená, že je rýchlejšie vylepšiť/upraviť obrázok v odtieňoch sivej, pretože je k dispozícii menej údajov, ktoré je potrebné sledovať. Na konverziu obrázka na stupne šedej použite rgb2gray. (Bola použitá funkcia imrotate, pretože naše fotografie boli horizontálne - tento riadok kódu môže, ale nemusí byť vo vašej verzii potrebný.)

• %previesť do stupňov šedej a otočiť
• I = imread (ControlFile);
• I = rgb2gray (I);
• I = imrotovať (I, 90);

Ďalej zobrazte obrázok. Funkcia subplot sa používa na to, aby testovací obrázok mohol byť v ďalších krokoch vedľa ovládacieho prvku.

• %zobrazenie
• postava 1);
• podkres (1, 2, 1)
• imshow (I);
• názov (Kontrolný súbor);

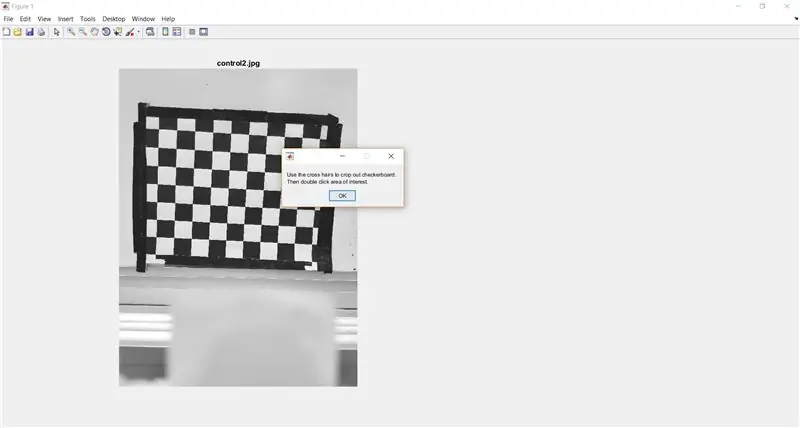
Použite imcrop na vyzvanie užívateľa, aby orezal šachovnicu z celého obrázku. Nasledujúci kód tiež zobrazuje okno so správou, ktoré má poskytnúť používateľovi pokyny.

• %výrez šachovnice na analýzu
• počkajte (msgbox ({'Použite krížiky na orezanie šachovnice.', 'Potom dvakrát kliknite na oblasť záujmu.'}));
• I_crop = imcrop (I);

Na binarizáciu obrázka použite imbinarize.

I_binary = imbinarize (I_crop);

Krok 4: Vypočítajte šírku bielych štvorcov na šachovnici

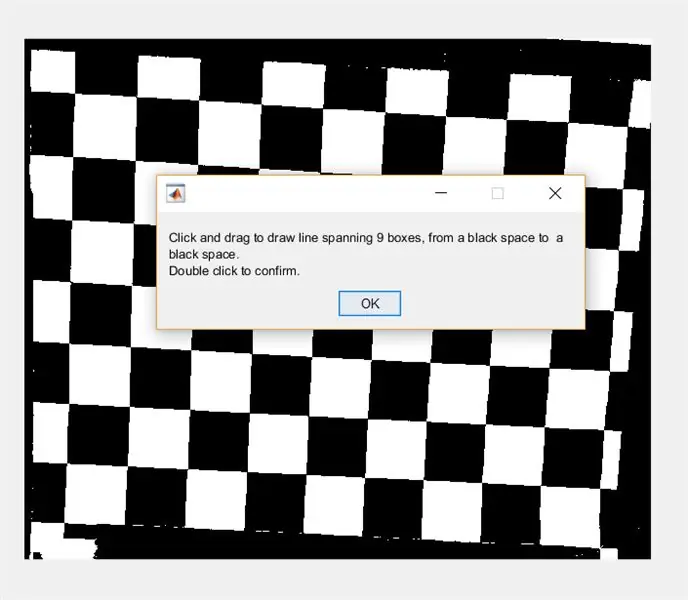
Ďalej vyzvite používateľa, aby nakreslil čiaru cez obrázok pomocou vloženia. Tento riadok by mal prebiehať vodorovne cez šachovnicu. Malo by to začať a skončiť na čiernom štvorci (nezáleží na tom, kde)- je to preto, že budeme merať šírku bielych štvorcov, nie čiernych.

• %rysovacej čiary
• postava 1)
• podkres (1, 2, 1)
• imshow (I_binary);
• čakať (msgbox ({'Kliknutím a potiahnutím nakreslite čiaru pokrývajúcu 9 polí, od čierneho priestoru po čierne miesto.', 'Dvojitým kliknutím potvrdíte.'}));
• riadok = imline;
• pozícia = čakať (riadok);
• koncové body = line.getPosition;

Extrahujte kodóny X a Y pre koncové body nakreslenej čiary.

• X = koncové body (:, 1)
• Y = koncové body (:, 2);

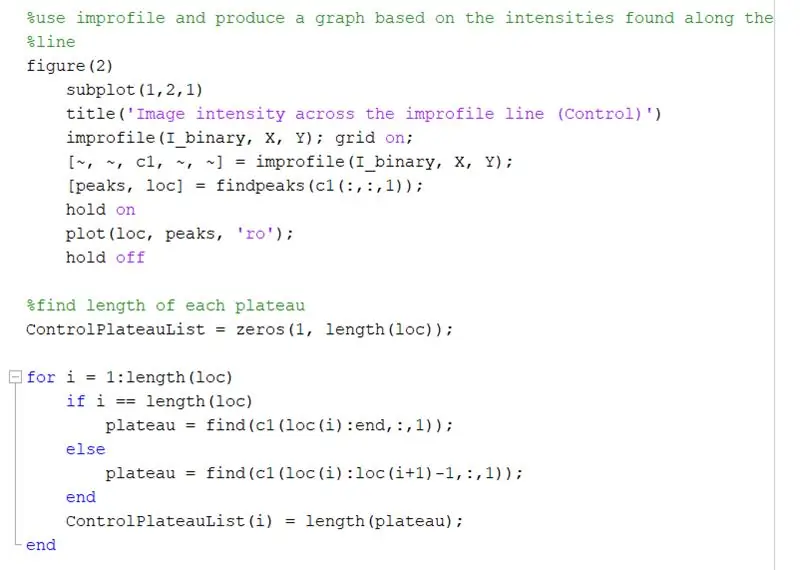
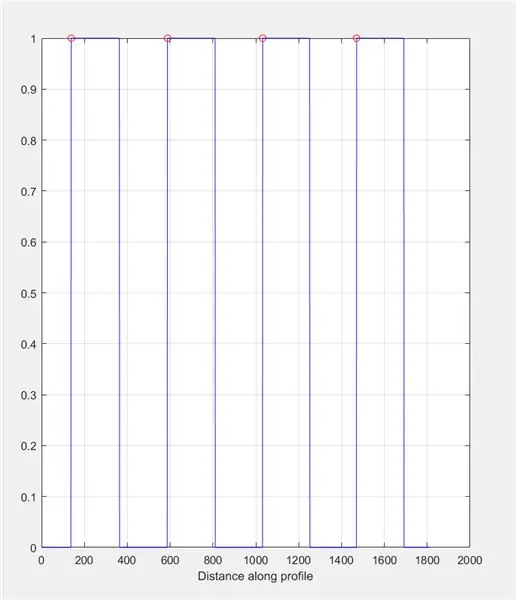
Použitím improfilu vytvorte graf na základe intenzít nachádzajúcich sa pozdĺž nakreslenej čiary. Malo by to pripomínať štvorcovú vlnu v rozsahu od 0 (čierna) do 1 (biela). Vypočítajte tiež vrcholy a ich polohy.

• figúrka (2)
• podkres (1, 2, 1)
• title ('Intenzita obrazu na neprofilnom riadku (kontrola)')
• neprofilný (I_binárny, X, Y); mriežka zapnutá;
• [~, ~, c1, ~, ~] = neprofil (I_binary, X, Y);
• [vrcholy, loc] = vrcholy nálezov (c1 (:,:, 1));
• Počkaj
• plot (miesto, vrcholy, 'ro');
• vydržať

Nájdite dĺžku každého plató na grafe neprofilu pomocou cyklu for. Spustite slučku for pre rovnaké množstvo vrcholov, aké sú v grafe neprofilu. Na výpočet dĺžky každého plató použite funkciu „nájsť“a nájdite všetky miesta, kde je „1“namiesto hodnoty intenzity „0“. Potom vypočítajte dĺžku tohto poľa, aby ste získali celkovú dĺžku plošiny, ktorá by sa mala rovnať šírke bieleho štvorca v pixeloch. ControlPlateauList = nuly (1, dĺžka (loc));

pre i = 1: dĺžka (loc)

ak i == dĺžka (loc)

plateau = find (c1 (loc (i): end,:, 1));

inak

plateau = find (c1 (loc (i): loc (i+1) -1,:, 1));

koniec

ControlPlateauList (i) = dĺžka (plató);

koniec

Krok 5: Opakujte kroky 3 a 4 pre testovací obrázok

*Poznámka: Pri kreslení neprofilnej čiary na testovací obrázok ju nakreslite cez štvorce, ktoré zodpovedajú čiare, ktorú ste nakreslili na kontrolný obrázok.

Krok 6: Vypočítajte zväčšenie objektívu

Zväčšené merania sa vypočítajú vydelením priemeru dĺžky plató, ktorý bol vypočítaný v kroku 5, priemerom dĺžky kontrolného plató, ktorý bol vypočítaný v kroku 4. Toto je vypočítané ako 1,0884.

zväčšenie = priemer (plateauList)/priemer (ControlPlateauList);

Krok 7: Nájdenie R-štvorca a predpisu používateľa prostredníctvom interpolácie

Použitie kódu:

• md1 = fitlm (GivenPrescription, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Môžeme nájsť R-štvorcovú hodnotu grafu GivenPresciption (hodnoty uvedené našimi šošovkami) vs. MagArray (sústava pomerov meraní zväčšenia, ktoré sme vypočítali skôr). Z dostatočne vysokej hodnoty R na druhú sa dá usúdiť, že existuje dostatočne silná korelácia, ktorá odôvodňuje použitie tejto metódy. V tomto konkrétnom prípade bola hodnota R-kvadrát 0,9912, čo naznačuje silnú koreláciu, a preto je opodstatnené pri použití tejto metódy v analýze.

Použitie funkcie:

Predpis = interp1 (MagArray, GivenPrescription, zväčšenie, 'lineárne');

Môžeme interpolovať zodpovedajúcu predpísanú hodnotu (na osi x) nášho pomeru zväčšenia (hodnota na osi y) a zistiť, aký je predpis používateľa.

Interpolácia údajov je dôležitá pre to, aby táto metóda fungovala, pretože nám umožňuje robiť predpoklady o informáciách, ktoré nemáme, na základe informácií, ktoré máme. Napriek tomu, že línia najlepšieho prispôsobenia by bola technicky silnejším kandidátom na tento predpoklad, vytvorenie hraníc na zníženie počtu výstupov má rovnaký účinok, ako keby dioptrické okuliare prichádzali v prírastkových jednotných hodnotách. To je vysvetlené v ďalších krokoch.

Krok 8: Zobrazenie predpisu používateľa na grafe

Pomocou nasledujúceho kódu:

• obrázok;
• sprisahanie (GivenPrescription, MagArray, '-g')
• Počkaj
• sprisahanie (predpis, zväčšenie, „bp“)
• vydržať
• mriežka
• legenda („Údaje“, „Interpolované body“, „Poloha“, „SZ“)

Môžeme vykresliť graf, ktorý ukazuje pomery zväčšenia oproti danému predpisu zelenou čiarou a nájdené údaje o našom vypočítanom zväčšení oproti nášmu interpolovanému predpisu s modrou hviezdou. Potom legenda označí názov, os x a os y a umiestni legendu do ľavého horného rohu.

Krok 9: Zúžte predpis

Na zaokrúhlenie predpisu sa používa nasledujúci kód:

• ak predpis <= 1,125

  CalculatedPrescription = '1,0';

• elseif Predpis <= 1,375

  CalculatedPrescription = '1,25';

• elseif Predpis <= 1,625

  CalculatedPrescription = '1,5';

• elseif Predpis <= 1,875

  CalculatedPrescription = '1,75';

• elseif Predpis <= 2.25

  CalculatedPrescription = '2,0';

• elseif Predpis <= 2,625

  CalculatedPrescription = '2,5';

• elseif Predpis <= 3

  CalculatedPrescription = '2,75';

• elseif Predpis <= 3,375

  CalculatedPrescription = '3,25';

• inak

  CalculatedPrescription = 'neznámy';

• koniec

Predpis nájdený prostredníctvom interpolácie nemusí nevyhnutne odrážať skutočný predpis - je to preto, že pri analýze fotografie v dôsledku ľudskej chyby budú vždy malé odchýlky. Tento krok teda potrebujeme na klasifikáciu skutočného predpisu.

Recepty, ktoré sa uvádzajú, zvyčajne začínajú od 1,0 dioptrie a v predpisoch sa zvyšujú o 0,25, takže po vypočítaní predpisu chceme určiť recept, ktorý najlepšie vyhovuje tomu, čo by užívateľ mohol potrebovať. Po výpočte predpisu ho prevedieme danými príkazmi If, aby sme skontrolovali jeho hodnotu a zistili, ktorý predpis je potrebný. Čokoľvek je menšie alebo rovné 1,125, potom predpis je 1,0. Čokoľvek je 1,375 alebo menej, predpis je 1,25. Čokoľvek je 1,625 alebo menej, predpis je 1,5. Čokoľvek je 1,845 alebo menej, predpis je 1,75. A tak ďalej.

Hodnoty sa nám zvyšujú, pretože kontrolujeme, či sú hodnoty menšie ako. Ak by sme urobili hodnoty klesajúce, potom prvý príkaz if by vždy čítal prvý príkaz if. Ak je predpis najmenší, chceme, aby ho ihneď rozpoznal ako najmenší, a preto je najmenšia hodnota tým, s čím sme začali. Čokoľvek vyššie ako najvyššia hodnota znamená, že predpis nie je v rozsahu s našimi údajmi, takže bude čítať reťazec „Neznámy“.