Riešenie tabuliek pravdy: 10 krokov

2025 Autor: John Day | [email protected]. Naposledy zmenené: 2025-01-23 15:05

Pravdivá tabuľka je spôsob, ako vizualizovať všetky výsledky problému. Táto inštrukčná sada je určená pre ľudí, ktorí začínajú s diskrétnou matematikou. Dnes budeme cvičiť s príkladom problému, ktorý je špecifický pre tieto pokyny. Na vizualizáciu stola budete potrebovať stierací papier a ceruzku. Tento problém by mal ľuďom s predchádzajúcimi znalosťami témy trvať asi 5 minút a začiatočníkom asi 10 minút.

V tejto množine inštrukcií sa zameriame na problém ~ p Λ q. Používame to na predstavenie niektorých symbolov potrebných na interpretáciu tabuliek pravdy.

Krok 1: Pochopenie tabuliek pravdy

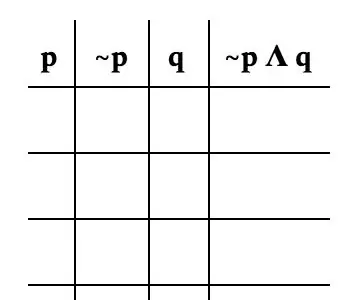
Pravdivá tabuľka je spôsob, ako si predstaviť všetky možnosti problému. Poznať pravdivostné tabuľky je základnou potrebou diskrétnej matematiky. Tu nájdeme všetky výsledky pre jednoduchú rovnicu ~ p Λ q.

Krok 2: Zoznámenie sa so symbolmi

Prvým krokom k tabuľke pravdy je porozumenie znameniam. „~“V tomto konkrétnom probléme znamená negáciu. „P“a „q“sú obe premenné. Znak „Λ“je ekvivalentom znamienka „a“. Táto rovnica sa číta ako „nie p a q“, čo znamená, že rovnica platí, ak p nie je pravdivé a q je pravdivé.

Krok 3: Formátovanie tabuľky

Teraz vytvorte skutočnú tabuľku. Je dôležité rozdeliť problém na každú premennú. Pre tento problém ho rozdelíme nasledovne: p, ~ p, q a ~ p Λ q. Obrázok je dobrým príkladom toho, ako by mal váš stôl vyzerať.

Krok 4: Priradenie pravdy a nepravdy

Pretože existujú iba dve premenné, budú existovať iba štyri možnosti pre každú premennú. Pre p rozdelíme na polovicu medzier, ktoré zaberá T (pre pravda), a druhú polovicu pre F (pre nepravdu).

Krok 5: Negácia

Pre ~ p napíšete opačné znamienko, ktoré má p, pretože ~ p je opakom p.

Krok 6: premenná „q“

V prípade q striedate T a F, aby ste získali každú možnú kombináciu. Pretože sa rovnica zameriava iba na ~ p, pri určovaní pravdivosti rovnice môžeme stĺpec p ignorovať. Symbol „Λ“znamená, že ~ p aj q musia byť pravdivé, aby bola rovnica pravdivá.

Krok 7: Riešenie nepravdivých informácií v poslednom stĺpci

V prvom riadku, pretože ~ p je F a q je T, ~ p Λ q je F v scenári, že ~ p je F a q je T. Jediný scenár, v ktorom je rovnica T, je ~ p je T a q je T.

Krok 8: Hľadanie pravdy v poslednom stĺpci

To znamená, že jediný riadok, ktorý je T, je tretí.

Krok 9: Dokončenie tabuľky

Znova skontrolujte, či je váš stôl správny. Vykonáte to tak, že skontrolujete správnosť značiek a uistíte sa, že posledný stĺpec je vykonaný správne. Posledný stĺpec je výsledkom všetkých možných permutácií z premenných.

Krok 10: Hotovo

Teraz, keď viete, ako vytvoriť základnú tabuľku pravdy, pokračujte v cvičení! Čím viac budete cvičiť, tým lepšie ich budete vykonávať.