Ako vytvoriť geodetický dóm v štýle Temcor v programe Autodesk Inventor: 8 krokov

2024 Autor: John Day | [email protected]. Naposledy zmenené: 2024-01-30 12:00

Tento tutoriál vám ukáže, ako vytvoriť kopulu v štýle Temcor len s trochou matematiky.

Väčšina informácií v tomto návode bola zhromaždená z reverzného inžinierstva TaffGocha o metódach delenia starej stanice južného pólu Amundsen-Scott, takže mu patrí veľká vďaka!

Hlavnou výhodou kupol Temcor je nízky počet unikátnych vzpier - aritmeticky sa zvyšuje s frekvenciou, nie na rozdiel od pravidelnej triakontaedrálnej geodetickej siete Duncana Stuarta (metóda 3*), ale výsledok vyzerá oveľa príjemnejšie.

Frekvencia kupoly, ktorú vyrábame, je pre jednoduchosť 14, takže akordové faktory je možné porovnať s modelom TaffGoch Temcor.

Inventor 2016.ipt je zahrnutý na konci tutoriálu.

*AKTUALIZÁCIA*

Metódu 4 som opísal ako pravidelnú triakontaedrálnu geodetickú mriežku Duncana Stuarta, ale nie je. Metódu skutočne vynašiel Christopher Kitrick, ktorý vo svojom príspevku z roku 1985 „Geodetické dómy“popísal jej stavbu. Okrem toho vo svojej práci z roku 1990 „Zjednotený prístup k geodetickým kopulám triedy I, II a III“načrtáva ďalších 8 metód, jednou z nich je metóda 3 Duncana Stuarta, druhou „metóda 4“a prekvapivo dosť, analogická metóda k spoločnosti Temcor's, ktorú nazýva „metóda aa“(krok 7 ukazuje, ako spoločnosť Temcor upravila „metódu aa“). V budúcnosti poučiteľný budem popisovať konštrukciu metód načrtnutých v tomto poslednom príspevku.

Krok 1: Používateľské parametre

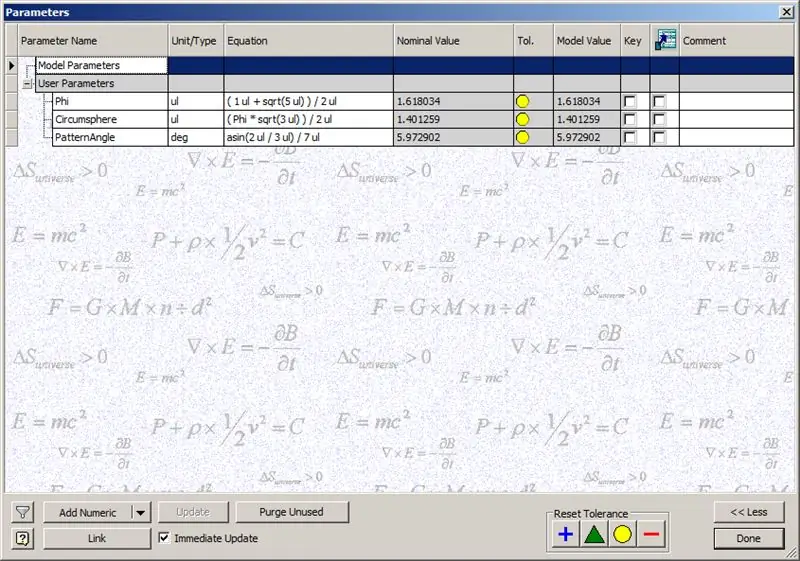
Predtým, ako sa pustíme do stavby kupoly, zadajte zobrazené parametre:

Phi - Zlatý pomer. Definované ako (((1+√5/) 2

Circumsphere - toto je cirkulárka dodekahedronu, definovaná ako ((Phi*√3)/2)

PatternAngle - Toto je stredový uhol dodekaedra. Pretože frekvencia našej kupoly je 14, delíme tento stredový uhol na polovicu frekvencie, v tomto prípade 7.

Krok 2: Načrtnutie zlatého obdĺžnika

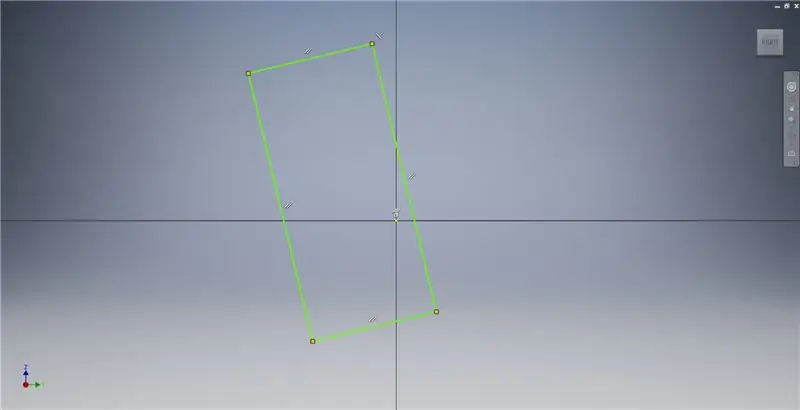
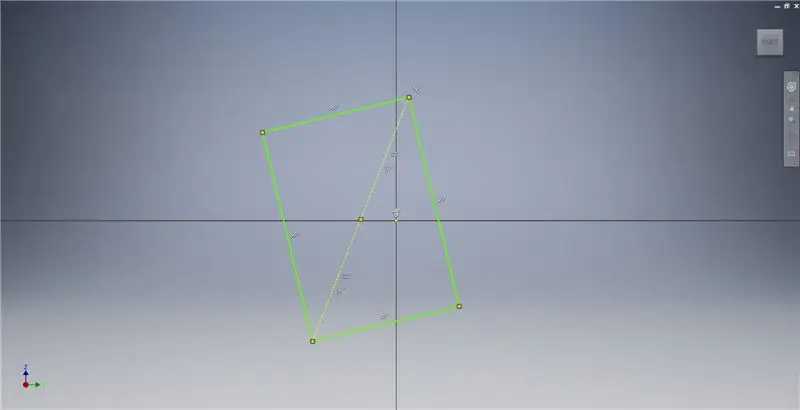
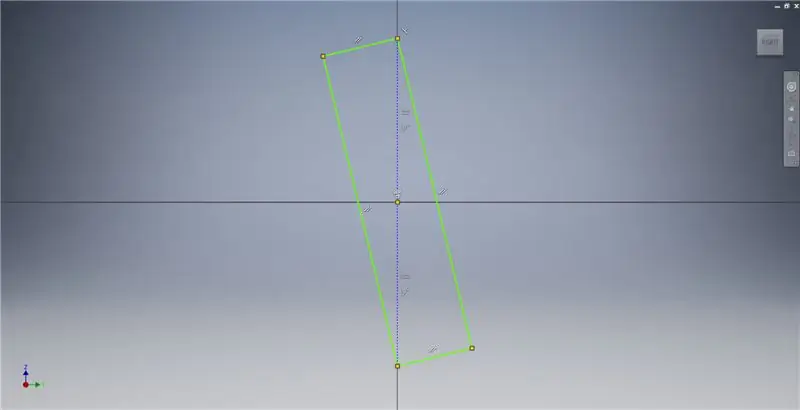
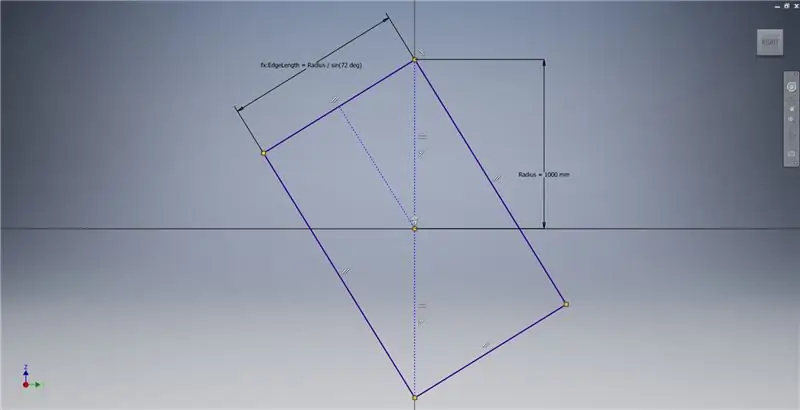
Začnite skicovaním v rovine YZ a potom vytvorte trojbodový obdĺžnik podľa obrázku. Ďalšie informácie o vytvorení zlatého obdĺžnika nájdete v poznámkach k obrázku.

Krok 3: Vytvorenie obdĺžnika Golden²

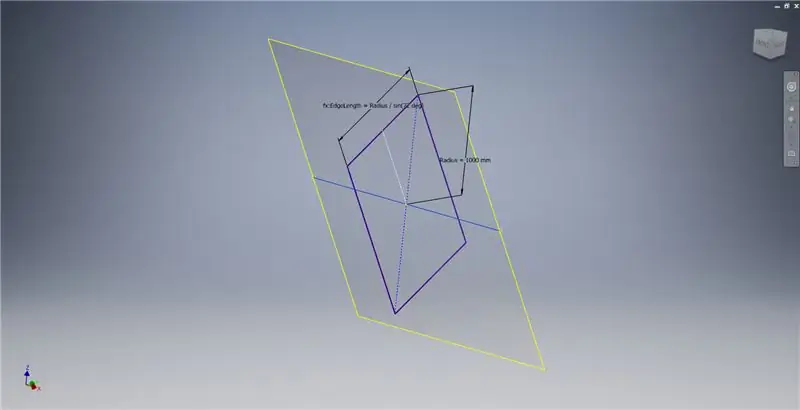
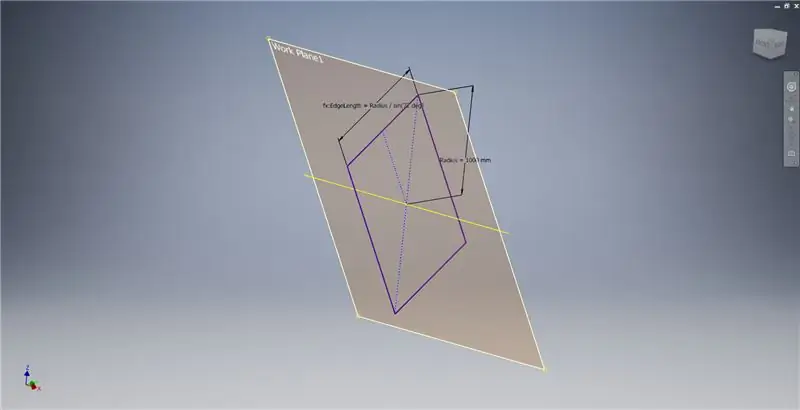
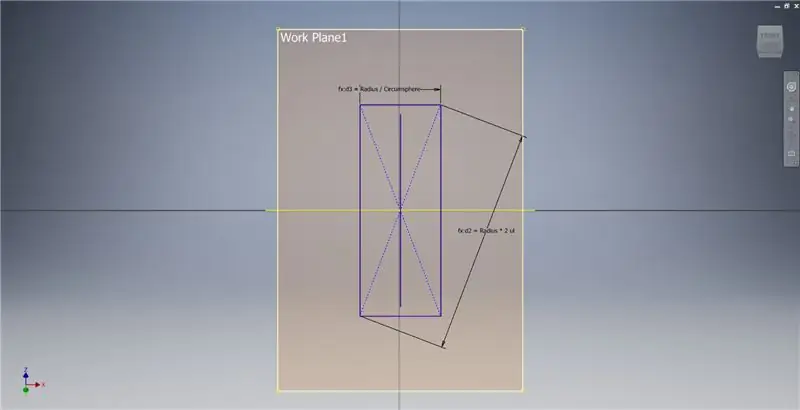
Vytvorte pracovnú rovinu pomocou osi X a čiary zvýraznenej na prvom obrázku, potom začnite ďalší náčrt tejto pracovnej roviny. Vytvorte obdĺžnik so stredovým bodom od začiatku a potom obdĺžnik okótujte podľa tretieho obrázku.

Krok 4: Vytvorenie 2v Triacon trojuholníka

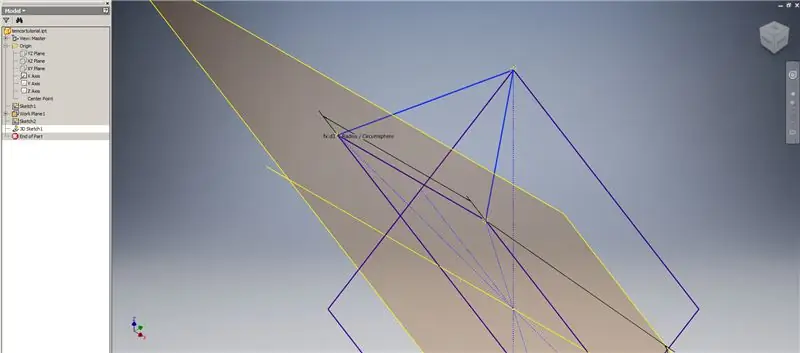
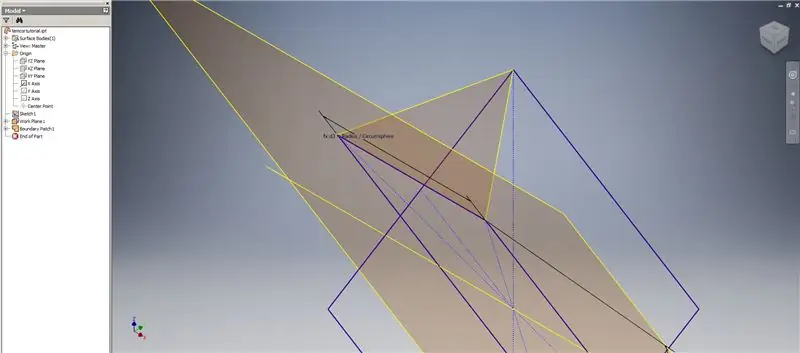
Teraz, keď máme všetku potrebnú geometriu, vytvorte hraničnú náplasť na druhom obrázku pomocou ľubovoľnej metódy, ktorú uprednostňujete. Rozhodol som sa urobiť 3D skicu, ale skicovanie v inej pracovnej rovine by fungovalo rovnako dobre.

Krok 5: Vytvorenie križovatkových rovín

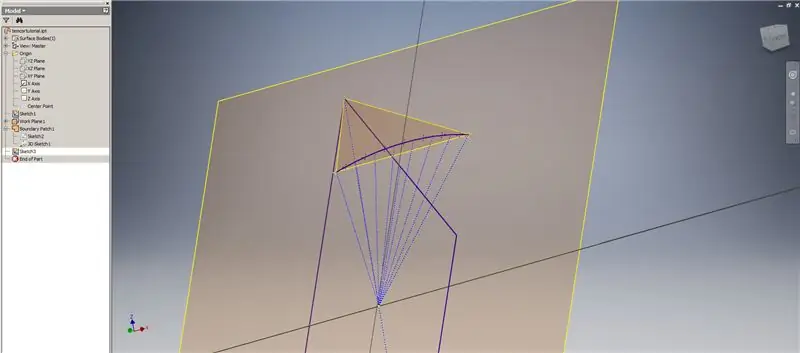
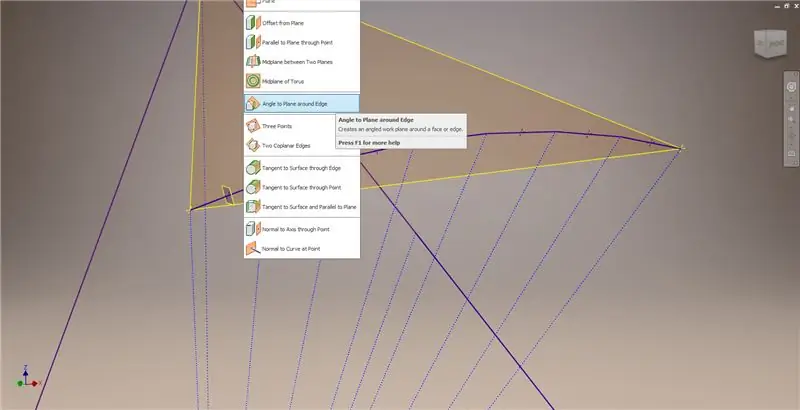
Začnite ďalším náčrtkom v prvej pracovnej rovine („Pracovná rovina 1“), ktorú ste vytvorili, premietnite rohy obdĺžnika Golden², potom spojte tieto body a počiatok a vytvorte stredový uhol 2v triacontahedronu. Rozdeľte ho na polovicu frekvencie kupoly, ako keby ste začínali rozpis podľa Metódy 2. Umiestnite body na stredové body akordov.

Ukončite náčrt a vytvorte rovinu pomocou jedného z akordov a jeho stredu, ako je znázornené na druhom obrázku. Potom vytvorte ďalšiu pracovnú rovinu pomocou možnosti „Uhol k rovine okolo okraja“. Vyberte pracovnú rovinu 1 a jednu z konštrukčných línií zobrazenú na obrázku vpravo dole a vľavo dole. Akceptujte predvolený uhol 90 stupňov, inak by zvyšok rozdelenia nevyzeral správne. Opakujte postup s použitím zvyšných akordov a konštrukčných čiar, aby ste získali výsledok na pravom dolnom obrázku.

Krok 6: Vytvorenie priesečníkových kriviek a vytvorenie podskupiny

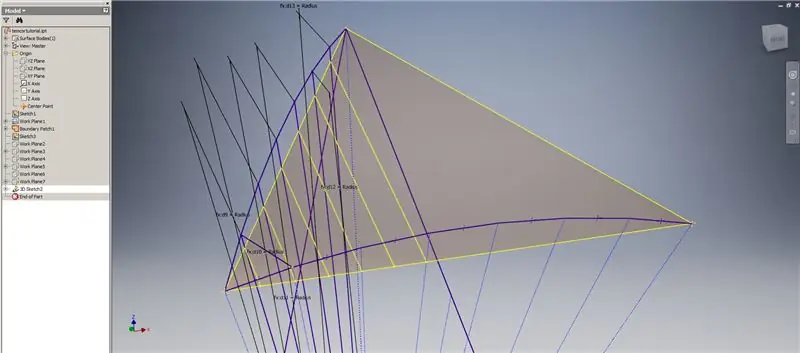
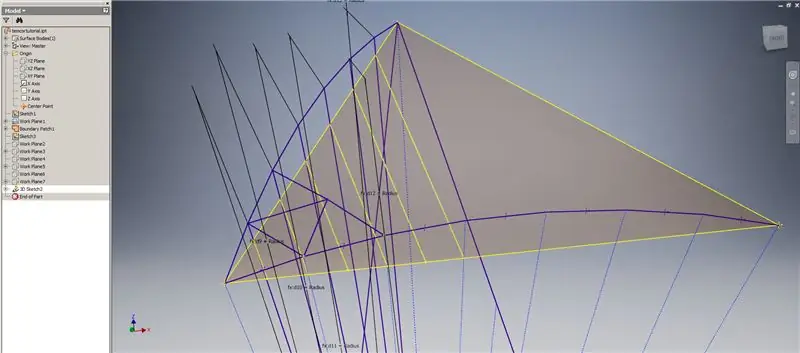
Spustite 3D skicu a potom vytvorte priesečníkové krivky pomocou pracovných rovín, ktoré ste práve vytvorili, a ohraničovacej záplaty, ktoré vytvoria čiary zobrazené na hornom obrázku.

Nakreslite čiary zhodné s koncovými bodmi priesečníkových kriviek, ako je to znázornené na obrázku 2. Zarovnajte ich s polomerom kupoly. Nakreslite akordy spájajúce čiary, ktoré ležia na priesečníkových krivkách. Spojte akúkoľvek geometriu, ktorá vyzerá dostatočne blízko, aby vytvoril trojuholník podskupiny. Pozrite sa na nasledujúcich 10 obrázkov, ktorých akordy sa majú zrkadliť naprieč rovinami pracovných priesečníkov - môžu to vysvetliť lepšie ako obyčajné slová.

Krok 7: Dokončenie kupoly

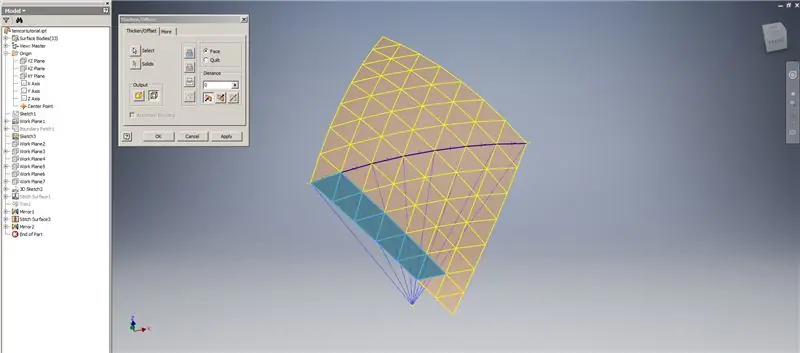
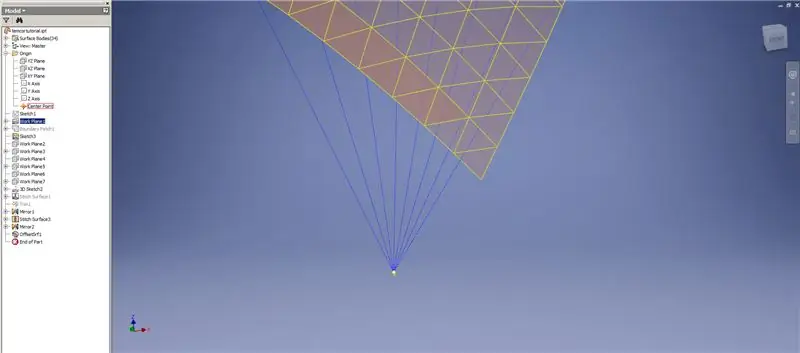
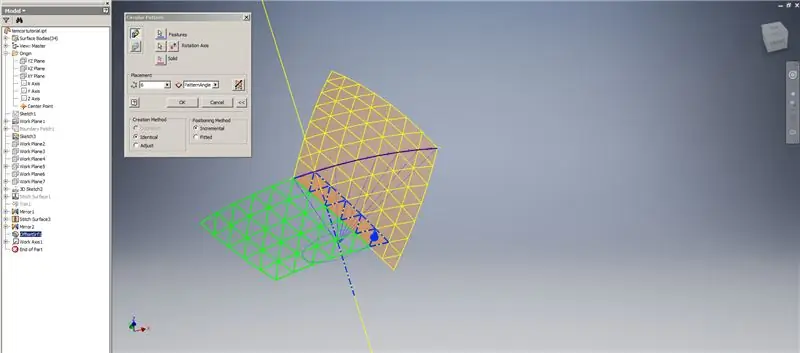
Vytvorte zahustenie/posunutie spodných riadkov, pričom vynechajte posledné dva rady trojuholníkov. Vzorujte nový OffsetSrf 6-krát alebo ((Frekvencia = 14)/2) -1. Skryte OffsetSrf, zošívajte vzorované povrchy a potom zošite zrkadlovo prešitý povrch pomocou roviny YZ. Vytvorte pracovné roviny ležiace na vrcholoch horného trojuholníka, ako je to znázornené na obrázku 6. Orežte zošité a zrkadlové povrchy pomocou týchto nových pracovných rovín a potom zostávajúce povrchy spojte dohromady. Vzorujte tento posledný povrch cez os Z, potom tieto konečné povrchy spojte dohromady a máte hotovo!

Krok 8: Kontrola akordov

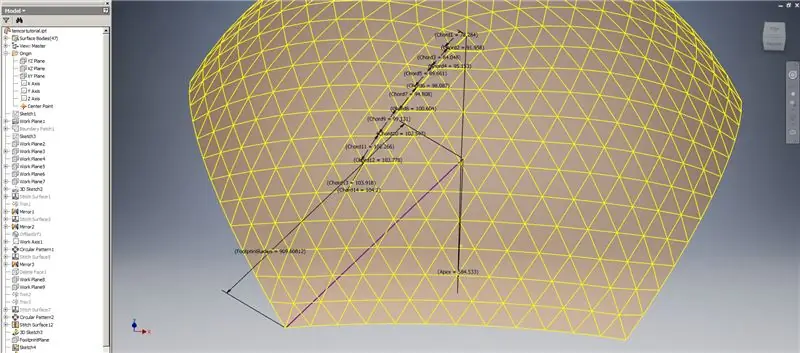
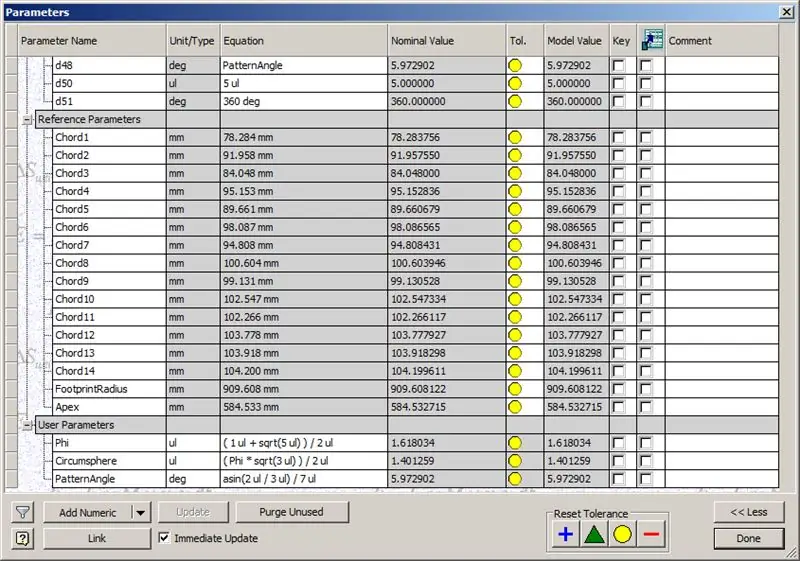
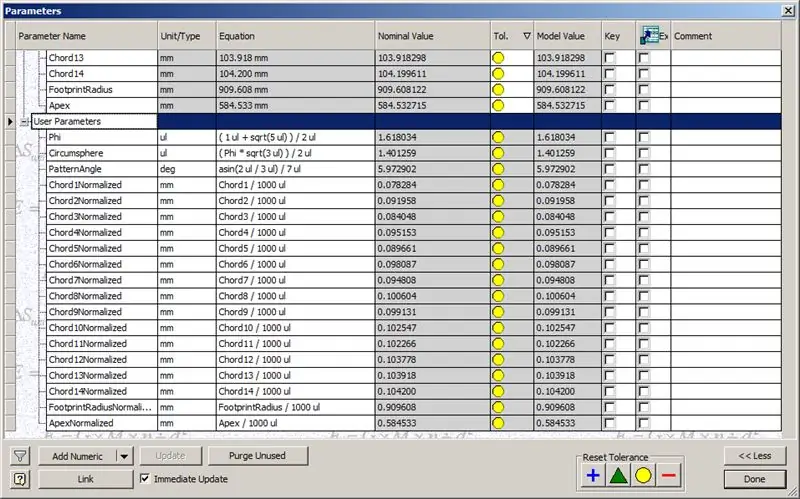
Naša kupola je teda hotová, ale pozrime sa, či sa čísla zhodujú s modelom TaffGocha:

Pokiaľ ide o referenčné parametre, zdá sa, že sa perfektne zhodujú!

Rozdelením akordových dĺžok na 1000 môžeme jasne vidieť dokonalú zhodu s akordickými faktormi TaffGochovho modelu, ako aj s polomerom stopy a faktormi vrcholu.