Samovyvažovací robot pomocou algoritmu PID (STM MC): 9 krokov

2024 Autor: John Day | [email protected]. Naposledy zmenené: 2024-01-30 12:00

V poslednej dobe sa vykonalo veľa práce na vlastnom vyvažovaní objektov. Koncept vlastného vyvažovania sa začal vyvážením obráteného kyvadla. Tento koncept sa rozšíril aj na dizajn lietadiel. V tomto projekte sme navrhli malý model samovyvažovacieho robota pomocou algoritmu PID (proporcionálny, integrálny, derivátový). Od tej doby je táto metóda novou tvárou systémov riadenia priemyselných procesov. Táto správa hodnotí metódy zahrnuté vo vlastnom vyvažovaní objektov. Tento projekt bol vedený ako semestrálny projekt s cieľom porozumieť korelácii PID s účinnosťou rôznych priemyselných procesov. Tu sa zameriavame iba na poskytnutie stručného prehľadu o účinnosti a použití PID riadenia. Tento dokument bol vyvinutý tak, že poskytuje stručný úvod do riadiacich systémov a súvisiace terminológie spolu s motiváciami projektu. Vykonali sa experimenty a pozorovania, popísali sa zásluhy a nedostatky a končili sa budúcimi zlepšeniami. Na pochopenie účinnosti PID vo svete riadiaceho systému bol vyvinutý model samovyvažovacieho robota. Po niekoľkých prísnych testoch a experimentoch sa zistili výhody a nevýhody riadiaceho systému PID. Zistilo sa, že napriek mnohým výhodám kontroly PID oproti predchádzajúcim metódam, tento systém stále vyžaduje veľa vylepšení. Dúfame, že čitateľ dobre porozumie dôležitosti vlastného vyvažovania, účinnosti a nedostatkom kontroly PID.

Krok 1: Úvod

S príchodom počítačov a industrializácie procesov v histórii človeka vždy existoval výskum s cieľom vyvinúť spôsoby, ako spresniť procesy, a čo je dôležitejšie, ovládať ich pomocou strojov autonómne. Cieľom je obmedziť zapojenie človeka do týchto procesov, a tým znížiť chyby v týchto procesoch. Preto bola vyvinutá oblasť „inžinierstva riadiacich systémov“. Inžinierstvo riadiaceho systému možno definovať ako používanie rôznych metód na riadenie fungovania procesu alebo udržiavanie konštantného a preferovaného prostredia, či už manuálneho alebo automatického.

Jednoduchým príkladom môže byť ovládanie teploty v miestnosti. Manuálne ovládanie znamená prítomnosť osoby na mieste, ktorá kontroluje súčasné podmienky (snímač), porovnáva ich s požadovanou hodnotou (spracovanie) a vykonáva potrebné opatrenia na získanie požadovanej hodnoty (ovládač). Problém tejto metódy je, že nie je veľmi spoľahlivá, pretože človek je vo svojej práci náchylný na chyby alebo nedbalosť. Ďalším problémom je tiež to, že rýchlosť procesu iniciovaného ovládačom nie je vždy jednotná, čo znamená, že niekedy môže prebiehať rýchlejšie, ako sa vyžaduje, alebo niekedy môže byť pomalý. Riešením tohto problému bolo použitie mikroovládača na ovládanie systému. Mikrokontrolér je

naprogramovaný na riadenie procesu podľa daných špecifikácií zapojený do obvodu (o ktorom bude reč neskôr), privádza požadovanú hodnotu alebo podmienky a tým riadi proces tak, aby udržal požadovanú hodnotu. Výhodou tohto postupu je, že do tohto procesu nie je potrebný žiadny ľudský zásah. Rýchlosť postupu je tiež jednotná

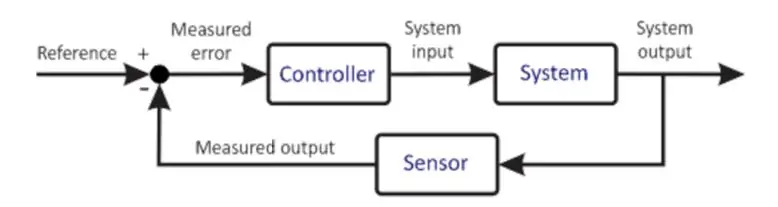
Základný riadiaci systém

Predchádzajúci diagram ukazuje veľmi zjednodušenú verziu riadiaceho systému. Mikrokontrolér je jadrom každého riadiaceho systému. Je to veľmi dôležitý komponent, preto by mal byť jeho výber vybraný starostlivo na základe požiadaviek systému. Mikroprocesor prijíma vstup od používateľa. Tento vstup definuje požadovaný stav systému. Mikroprocesor tiež získava spätnú väzbu od snímača. Tento senzor je pripojený k výstupu systému, ktorého informácie sú dodávané späť na vstup. Mikroprocesor na základe svojho programovania vykonáva rôzne výpočty a vydáva výstup pre akčný člen. Pohon na základe výkonu riadi zariadenie, aby sa pokúsil udržať tieto podmienky. Príkladom môže byť vodič motora poháňajúci motor, kde ovládač motora je pohon a motor je závod. Motor sa teda otáča danou rýchlosťou. Pripojený snímač sníma aktuálny stav zariadenia a napája ho späť do mikrokontroléra. Mikroprocesor opäť porovnáva, robí výpočty a cyklus sa teda opakuje. Tento proces sa opakuje a je nekonečný, pričom mikro-regulátor udržuje požadované podmienky

Krok 2: Riadiaci systém založený na PID

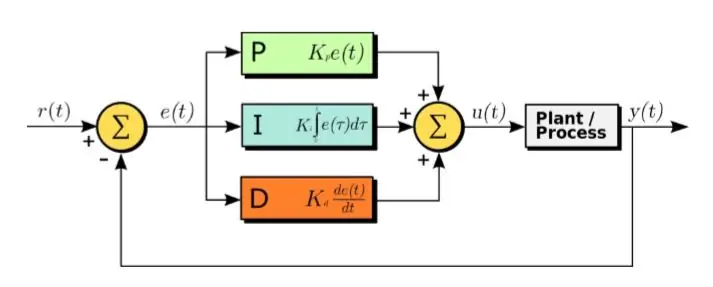
Algoritmus PID je účinnou metódou navrhovania riadiaceho systému.

Definícia

PID znamená proporcionálne, integrálne a derivačné. V tomto algoritme je vstupným signálom chybového signálu. Nasledujúca rovnica sa aplikuje na chybový signál

U (t) = Kp ∗ e (t) + Kd ∗ d/dt (e (t)) + Ki ∗ integrál (e (t)) (1,1)

Stručné vysvetlenie

Ako je zrejmé z vyššie uvedenej rovnice, integrál a derivácia chybových signálov sa vypočítajú, vynásobia ich príslušnými konštantami a sčítajú sa s konštantou Kp vynásobenou e (t). Výstup je potom privedený do akčného člena, ktorý spustí systém. Teraz sa pozrime na každú časť funkcie postupne. Táto funkcia priamo ovplyvňuje čas nábehu, pád, špičku nad záberom, čas ustálenia a chybu ustáleného stavu.

• Proporcionálna časť: Proporcionálna časť skracuje čas nábehu a znižuje chybu ustáleného stavu. To znamená, že systému bude trvať kratší čas, kým dosiahne svoju špičkovú hodnotu, a keď dosiahne svoj ustálený stav, chyba ustáleného stavu bude nízka. Zvyšuje však prekročenie vrcholu.

• Odvodená časť: Odvodená časť skracuje prestreľovanie a dobu usadzovania. To znamená, že prechodný stav systému bude viac tlmený. Systém tiež dosiahne svoj ustálený stav za kratší čas. Nemá to však žiadny vplyv na dobu nábehu alebo chybu ustáleného stavu.

• Integrovaná časť: Integrovaná časť skracuje dobu nábehu a úplne eliminuje chybu ustáleného stavu. Zvyšuje však prekročenie špičky a čas usadenia.

• Ladenie: Dobrý riadiaci systém bude mať nízky čas nábehu, čas ustálenia, prekročenie špičky a chybu ustáleného stavu. Preto je potrebné, aby Kp, Kd, Ki boli dôkladne vyladené tak, aby upravili príspevok vyššie uvedených faktorov, aby získali dobrý kontrolný systém.

Priložený obrázok ukazuje účinok zmeny rôznych parametrov v algoritme PID.

Krok 3: Samovyvažovací robot

Samovyvažovací robot je viacvrstvový dvojkolesový robot.

Robot sa pokúsi udržať rovnováhu pri použití akejkoľvek nerovnakej sily (síl). Vyrovnáva sa sám pôsobením sily, ktorá je proti výslednici síl na robota.

Metódy vlastného vyváženia

Existujú štyri spôsoby vlastného vyvažovania robotov. Ide o nasledujúce:

Samovyvažovanie pomocou dvoch infračervených snímačov náklonu

Toto je jeden z najhrubších spôsobov vyváženia robota, pretože vyžaduje oveľa menej hardvéru a relatívne ľahký algoritmus. Pri tomto prístupe sa na meranie vzdialenosti medzi zemou a robotom používajú dva naklonené infračervené senzory. Na základe vypočítanej vzdialenosti je možné PID použiť na pohon motorov na zodpovedajúce vyváženie robota. Jednou nevýhodou tejto metódy je, že IR snímač môže vynechať niektoré hodnoty. Ďalším problémom je, že na výpočet vzdialenosti je potrebné prerušenie a slučky, čo zvyšuje časovú zložitosť algoritmu. Tento spôsob vyvažovacieho robota preto nie je taký účinný.

Samovyvažovanie pomocou akcelerometra

Akcelerometer nám dáva zrýchlenie tela v 3 osiach. Zrýchlenie orientované v osi y (nahor) a osi x (vpred) nám dáva mieru na výpočet smeru gravitácie, a teda na výpočet uhla sklonu. Uhol sa vypočíta takto:

θ = arktán (Ay/Ax) (1,2)

Nevýhodou použitia tejto metódy je, že počas pohybu robota sa k hodnotám pridá aj horizontálne zrýchlenie, čo je vysokofrekvenčný šum. Uhol sklonu bude preto nepresný.

Samovyvažovanie pomocou gyroskopu

Na výpočet uhlových rýchlostí pozdĺž troch osí sa používa gyroskop. Uhol sklonu sa získa pomocou nasledujúcej rovnice.

θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1,3)

Jednou veľkou nevýhodou použitia gyroskopu je to, že má malý DC Bias, čo je nízkofrekvenčný šum a za niekoľko času sú vrátené hodnoty úplne nesprávne. To po integrácii spôsobí posunutie nulového bodu. V dôsledku toho zostane robot nejaký čas vo zvislej polohe a prevráti sa, keď príde drift.

Samovyvažovanie pomocou akcelerometra aj gyroskopu

Ako je uvedené vyššie, použitie iba akcelerometra alebo gyroskopu nám neposkytne správny uhol sklonu. Na tento účel sa používa akcelerometer a gyroskop. Oba sú integrované v MPU6050. V tomto prípade získavame údaje od oboch z nich a potom ich spájame buď pomocou Kalmanovho filtra, alebo doplnkového filtra.

• Kalmanov filter: Kalmanov filter vypočítava najlepší odhad stavu dynamického systému z hlučných meraní, pričom minimalizuje priemernú kvadratickú chybu odhadu. Operuje v dvoch fázach, predikcii a korekcii, vzhľadom na diskrétne stochastické rovnice popisujúce dynamiku systému. Je to však veľmi zložitý algoritmus, ktorý je možné implementovať najmä na obmedzenom hardvéri mikrokontroléra.

• Doplnkový filter: Tento algoritmus primárne používa údaje získané z gyroskopu a v priebehu času ich integruje, aby získal uhol sklonu. Tiež používa malý podiel hodnôt akcelerometra. Doplnkový filter v skutočnosti minimalizuje vysokofrekvenčný hluk akcelerometra a nízkofrekvenčný šum gyroskopu a potom ich spojí, aby poskytol čo najpresnejší uhol sklonu.

Krok 4: Návrh robota

Navrhli sme samovyvažovacieho robota s použitím proporcionálneho derivačného regulátora implementovaného doplnkovým filtrom pre MPU6050. Tento malý model samovyvažovacieho robota nám ukáže užitočnosť riadiacich systémov pri samovyvažovaní robotov.

Implementácia systému:

Systém je samovyvažovací robot. Implementuje sa pomocou regulátora PID, ktorý je proporcionálnym integrovaným derivačným regulátorom. Vyvažujeme robota poháňaním jeho kolies v smere jeho pádu. Pri tom sa snažíme udržať ťažisko robota nad otočným bodom. Aby sme poháňali kolesá v smere jeho pádu, mali by sme vedieť, kam robot padá a akú rýchlosťou padá. Tieto údaje sa získavajú pomocou MPU6050, ktorý má akcelerometer a gyroskop. MPU6050 meria uhol sklonu a dáva výstup mikrokontroléru. MPU6050 je prepojený s doskou STM cez I2C. V I2C je jeden vodič pre hodiny, ktorý je pomenovaný ako SCL. Ten druhý je na prenos údajov, ktorý je SDA. V tomto prípade sa používa komunikácia master -slave. Počiatočná a koncová adresa je špecifikovaná tak, aby vedela, odkiaľ údaje začínajú a kde končia. Tu sme implementovali doplnkový filter pre MPU6050, čo je matematický filter na zlúčenie výstupov akcelerometra a gyroskopu. Po získaní údajov z MPU6050 bude mikrokontrolér vykonávať výpočty, aby vedel, kam padá. Na základe výpočtov bude mikroovládač STM dávať vodičovi motora príkazy na riadenie vozidiel v smere pádu, čo vyváži robota.

Krok 5: Komponenty projektu

V projekte samovyvažovacieho robota boli použité nasledujúce komponenty:

STM32F407

Mikroprocesor navrhnutý spoločnosťou ST Microelectronics. Funguje na architektúre ARM Cortex-M.

Ovládač motora L298N

Tento integrovaný obvod sa používa na chod motora. Má dva externé vstupy. Jeden z mikrokontroléra, ktorý mu dodáva signál PWM. Nastavením šírky impulzu je možné nastaviť otáčky motora. Jeho druhým vstupom je zdroj napätia potrebný na pohon motora, ktorým je v našom prípade batéria 12V.

DC motor

Jednosmerný motor beží na jednosmernom napájaní. V tomto experimente DC motor beží pomocou optočlenov pripojených k ovládaču motora. Na pohon motora sme použili Motor Drive L298N.

MPU6050

MPU6050 sa používa na získanie informácií o tom, kde robot padá. Meria uhol sklonu vzhľadom na bod nulového sklonu, čo je poloha MPU6050 pri spustení programu.

MPU6050 má 3-osový akcelerometer a 3-osový gyroskop. Akcelerometer meria zrýchlenie pozdĺž troch osí a gyroskop meria uhlovú rýchlosť okolo troch osí. Aby sme spojili výstup, musíme filtrovať zvuky oboch. Na odfiltrovanie zvukov máme Kalmanov a doplnkový filter. Do nášho projektu sme implementovali doplnkový filter.

Opto pár 4N35

Optočlen je zariadenie používané na izoláciu nízkonapäťovej a vysokonapäťovej časti obvodu. Ako naznačuje názov, funguje na základe svetla. Keď časť nízkeho napätia dostane signál, prúd prúdi v časti vysokého napätia

Krok 6: Štruktúra robota

Štruktúra robota je vysvetlená nasledovne:

Fyzická štruktúra

Samovyvažovací robot sa skladá z dvoch vrstiev z priehľadného plastového skla. Podrobnosti o dvoch vrstvách sú uvedené nižšie:

Prvá vrstva

V spodnej časti prvej vrstvy sme umiestnili článok na napájanie dosky STM. Na každú stranu boli tiež umiestnené dva 4 voltové motory s pneumatikami spojenými, aby sa robot mohol pohybovať. V hornej časti prvej vrstvy sú na prevádzku motorov umiestnené dve batérie, každá s napätím 4 volty (celkom 8 voltov) a integrovaným obvodom vodiča motora (L298N).

Druhá vrstva

V hornej vrstve robota sme umiestnili dosku STM na dosku Perf. Na vrchnú vrstvu je umiestnená ďalšia doska pre perfekciu zo 4 opto spojok. Gyroskop je tiež umiestnený na hornú vrstvu robota zo spodnej strany. Oba komponenty sú umiestnené v strednej časti tak, aby bolo ťažisko čo najnižšie.

Ťažisko robota

Ťažisko je udržiavané čo najnižšie. Za týmto účelom sme na spodnú vrstvu umiestnili ťažké batérie a na hornú vrstvu ľahké komponenty, ako sú doska STM a optočleny.

Krok 7: Kód

Kód bol zostavený na serveri Atollic TrueStudio. Na ladenie bolo použité STM studio.

Krok 8: Záver

Po veľkom experimentovaní a pozorovaní sa nakoniec dostávame k bodu, kde sumarizujeme naše výsledky a diskutujeme o tom, ako ďaleko sa nám podarilo implementovať a vypracovať efektivitu systému.

Všeobecná kontrola

Počas experimentovania bola rýchlosť motora úspešne riadená pomocou algoritmu PID. Krivka však nie je úplne hladká rovná čiara. Existuje mnoho dôvodov:

• Senzor, aj keď je pripojený k nízkopriepustnému filtru, stále poskytuje určité konečné odbúranie; tieto sú spôsobené nelineárnymi odpormi a niektorými nevyhnutnými dôvodmi analógovej elektroniky.

• Motor sa neotáča hladko pri malom napätí alebo PWM. Poskytuje trhania, ktoré by mohli spôsobiť nesprávne zadanie hodnôt do systému.

• Vzhľadom na kolísanie môže snímač vynechať niektoré štrbiny poskytujúce vyššie hodnoty. • Ďalším hlavným dôvodom chýb môže byť základná taktovacia frekvencia mikrokontroléra STM. Tento model mikrokontroléra STM ponúka takt jadra 168 MHz. Napriek tomu, že sa tento problém v tomto projekte zaoberá, existuje všeobecná predstava o tomto modeli, že neposkytuje takú vysokú frekvenciu.

Rýchlosť otvorenej slučky poskytuje veľmi plynulú čiaru iba s niekoľkými neočakávanými hodnotami. Algoritmus PID funguje aj vtedy, keď poskytuje veľmi nízky čas usadzovania motora. Algoritmus PID motora bol testovaný pri rôznych napätiach pri zachovaní konštantných referenčných otáčok. Zmena napätia nemení otáčky motora, čo ukazuje, že algoritmus PID funguje dobre

Účinnosť

Tu diskutujeme o účinnosti regulátora PID, ktorý sme pozorovali počas experimentovania.

Jednoduchá implementácia

V sekcii experimentovania a pozorovania sme videli, že regulátor PID je veľmi ľahko implementovateľný. Na to, aby mal systém riadenia rýchlosti, sú potrebné iba tri parametre alebo konštanty, ktoré je potrebné nastaviť

Bezkonkurenčná účinnosť pre lineárne systémy

Lineárny PID regulátor je najúčinnejší v rade regulátorov, pretože logika je veľmi jednoduchá a aplikácia je rozšírená v prípade lineárnych alebo dosť lineárnych aplikácií.

Obmedzenia

Abstraktne sme vysvetlili obmedzenia tohto systému. Tu diskutujeme o niekoľkých z nich, ktoré sme pozorovali.

Výber konštánt

Videli sme, že hoci je regulátor PID ľahko implementovateľný, stále je hlavnou nevýhodou systému, že krok výberu hodnoty konštánt je namáhavý; pretože je potrebné vykonať ťažké výpočty. Druhým spôsobom je metóda pokusu a pokusu, ale to tiež nie je účinné.

Konštanty nie sú vždy konštantné

Experimentálne výsledky ukázali, že pre rôzne hodnoty referenčných otáčok motora zlyhal PID regulátor pre rovnaké hodnoty konštánt PID. Pre rôzne rýchlosti museli byť konštanty zvolené odlišne a to exponenciálne zvyšuje náklady na výpočet.

Nelineárne

Regulátor PID používaný v našom prípade je lineárny, preto ho možno použiť iba na lineárne systémy. V prípade nelineárnych systémov je potrebné regulátor implementovať odlišne. Aj keď sú k dispozícii rôzne nelineárne metódy PID, vyžadujú si výber viacerých parametrov. To opäť robí systém nežiaducim z dôvodu vysokých výpočtových nákladov.

Vyžaduje sa počiatočné stlačenie

V experimentálnej časti sme ukázali, že pre pomerne malú referenčnú rýchlosť, kde je chyba na začiatku pomerne malá, je PWM dodávaný PID taký malý, že nevytvára požadovaný štartovací moment pre motor. Motor teda pri niektorých pokusoch nebeží alebo pri iných pokusoch poskytuje veľké prekročenie a dlhší čas usadzovania.

Krok 9: Osobitné poďakovanie

Osobitné poďakovanie patrí členom mojej skupiny, ktorí mi pomohli pri realizácii tohto projektu.

Odkaz na video vložím čoskoro.

Dúfam, že vás tento návod bude zaujímať.

Toto je Tahir Ul Haq z UET, ktorý sa odhlasuje. Na zdravie !!!