
Obsah:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 12:02.
- Naposledy zmenené 2025-01-23 15:07.
Úvod
Táto príručka je určená každému, koho zaujíma používanie akcelerometrov a gyroskopov, ako aj kombinovaných zariadení IMU (jednotka inerciálneho merania) pri projektoch elektroniky
Pokryjeme:
- Čo meria akcelerometer?
- Čo meria gyroskop (alias gyroskop)?
- Ako prevádzať údaje z analógového na digitálne (ADC), ktoré získate z týchto senzorov, na fyzické jednotky (to by bolo g pre akcelerometer, deg/s pre gyroskop)
- Ako skombinovať namerané hodnoty z akcelerometra a gyroskopu, aby ste získali presné informácie o sklone vášho zariadenia voči základnej rovine
V celom článku sa pokúsim obmedziť matematiku na minimum. Ak viete, čo sú Sine/Cosine/Tangent, mali by ste byť schopní porozumieť týmto myšlienkam a použiť ich vo svojom projekte bez ohľadu na to, akú platformu používate: Arduino, Propeller, Basic Stamp, Atmel čipy, Microchip PIC atď.
Existujú ľudia, ktorí veria, že na použitie jednotky IMU potrebujete komplexnú matematiku (komplexné filtre FIR alebo IIR, ako sú Kalmanov filtre, Parks-McClellan filtre atď.). Môžete ich preskúmať a dosiahnuť úžasné, ale komplexné výsledky. Môj spôsob vysvetľovania vecí vyžaduje iba základnú matematiku. Verím v jednoduchosť. Myslím si, že systém, ktorý je jednoduchý, sa ľahšie ovláda a monitoruje, okrem toho, že mnohé vstavané zariadenia nemajú dostatok energie a zdrojov na implementáciu komplexných algoritmov vyžadujúcich maticové výpočty.
Ako príklad použijem novú jednotku IMU, Acc_Gyro Accelerometer + Gyro IMU. Parametre tohto zariadenia použijeme v nižšie uvedených príkladoch. Táto jednotka je na začiatok dobrým zariadením, pretože pozostáva z 2 zariadení:
- LIS331AL (list s údajmi) - trojosový akcelerometer 2G - LPR550AL (list s údajmi) - dvojosový gyroskop s rozstupom a otáčaním, 500 stupňov/s
Spolu predstavujú 5-stupňovú jednotku inerciálneho merania slobody. Teraz je to vymyslené meno! Napriek tomu sa za efektným názvom skrýva veľmi užitočné kombinované zariadenie, ktorému sa v tejto príručke podrobne venujeme a vysvetlíme.
Krok 1: Akcelerometer
Aby sme pochopili túto jednotku, začneme akcelerometrom. Keď uvažujete o akcelerometroch, často je užitočné predstaviť si krabičku v tvare kocky s loptou vo vnútri. Môžete si predstaviť niečo iné ako sušienku alebo šišku, ale ja si predstavím loptu:
Ak vezmeme túto škatuľu na miesto bez gravitačných polí alebo bez ďalších polí, ktoré by mohli ovplyvniť polohu lopty - lopta jednoducho bude plávať v strede poľa. Môžete si predstaviť, že schránka je vo vesmíre ďaleko od akýchkoľvek kozmických telies, alebo ak je také miesto ťažké nájsť, predstavte si aspoň vesmírne plavidlo obiehajúce okolo planéty, kde je všetko v beztiažovom stave. Z obrázku vyššie vidíte, že ku každej osi priradíme pár stien (odstránili sme stenu Y+, aby sme sa mohli pozrieť do vnútra škatule). Predstavte si, že každá stena je citlivá na tlak. Ak zrazu pohneme škatuľou doľava (zrýchlime ju zrýchlením 1g = 9,8m/s^2), loptička narazí do steny X-. Potom zmeriame tlakovú silu, ktorou guľa pôsobí na stenu, a na osi X vydáme hodnotu -1g.
Uvedomte si, že akcelerometer skutočne detekuje silu, ktorá je nasmerovaná v opačnom smere od vektora zrýchlenia. Táto sila sa často nazýva inerciálna sila alebo fiktívna sila. Jedna vec, ktorú by ste sa z toho mali naučiť, je, že akcelerometer meria zrýchlenie nepriamo pomocou sily, ktorá je aplikovaná na jednu z jeho stien (podľa nášho modelu to môže byť pružina alebo niečo iné v akcelerometroch v reálnom živote). Táto sila môže byť spôsobená zrýchlením, ale ako uvidíme v nasledujúcom príklade, nie je vždy spôsobená zrýchlením.
Ak vezmeme náš model a umiestnime ho na Zem, guľa dopadne na stenu Z a na spodnú stenu bude pôsobiť silou 1 g, ako je znázornené na obrázku nižšie:
V tomto prípade sa pole nepohybuje, ale stále máme hodnotu -1g na osi Z. Tlak, ktorý lopta vyvinula na stenu, bol spôsobený gravitačnou silou. Teoreticky to môže byť iný typ sily - napríklad ak si predstavíte, že naša loptička je kovová, umiestnením magnetu vedľa škatule by sa loptička mohla posunúť tak, aby zasiahla inú stenu. Toto bolo povedané len preto, aby dokázal, že akcelerometer v podstate meria silu, nie zrýchlenie. Stáva sa, že zrýchlenie spôsobuje zotrvačnú silu, ktorá je zachytená mechanizmom detekcie síl akcelerometra.
Aj keď tento model nie je presne taký, ako je konštruovaný snímač MEMS, je často užitočný pri riešení problémov súvisiacich s akcelerometrom. V skutočnosti existujú podobné snímače, ktoré majú vo vnútri kovové guľôčky, nazývajú sa prepínače náklonu, sú však primitívnejšie a zvyčajne dokážu určiť iba to, či je zariadenie naklonené v určitom rozsahu alebo nie, nie rozsah sklonu.
Doteraz sme analyzovali výstup akcelerometra na jednej osi a to je všetko, čo získate s jednoosým akcelerometrom. Skutočná hodnota trojosových akcelerometrov pochádza zo skutočnosti, že dokážu detekovať zotrvačné sily vo všetkých troch osiach. Vráťme sa k nášmu modelu škatule a otočme box o 45 stupňov doprava. Lopta sa teraz dotkne 2 stien: Z- a X-, ako je znázornené na obrázku nižšie:
Hodnoty 0,71 nie sú ľubovoľné, sú to vlastne aproximácie pre SQRT (1/2). To bude jasnejšie, keď predstavíme náš ďalší model pre akcelerometer.
V predchádzajúcom modeli sme fixovali gravitačnú silu a otočili našu imaginárnu škatuľu. V posledných 2 príkladoch sme analyzovali výstup v 2 rôznych polohách boxu, pričom vektor sily zostal konštantný. Aj keď to bolo užitočné pri pochopení interakcie akcelerometra s vonkajšími silami, je praktickejšie vykonávať výpočty, ak súradnicový systém pripevníme k osiam akcelerometra a predstavíme si, že vektor síl sa otáča okolo nás.
Pozrite sa na vyššie uvedený model, zachoval som farby osí, aby ste mohli mentálne prejsť z predchádzajúceho modelu na nový. Predstavte si, že každá os v novom modeli je kolmá na príslušné plochy škatule v predchádzajúcom modeli. Vektor R je vektor sily, ktorý meria akcelerometer (môže to byť buď gravitačná sila alebo zotrvačná sila z vyššie uvedených príkladov alebo ich kombinácia). Rx, Ry, Rz sú projekciou vektora R na osi X, Y, Z. Všimnite si nasledujúceho vzťahu:
R^2 = Rx^2 + Ry^2 + Rz^2 (rov. 1)
čo je v zásade ekvivalent Pytagorovej vety v 3D.
Pamätajte si, že o niečo skôr som vám povedal, že hodnoty SQRT (1/2) ~ 0,71 nie sú náhodné. Ak ich zapojíte do vyššie uvedeného vzorca, po pripomenutí, že naša gravitačná sila bola 1 g, môžeme overiť, že:
1^2 = (-SQRT (1/2))^2 + 0^2 + (-SQRT (1/2))^2
jednoducho nahradením R = 1, Rx = -SQRT (1/2), Ry = 0, Rz = -SQRT (1/2) v Rovnici 1
Po dlhej preambule teórie sa dostávame bližšie k akcelerometrom v reálnom živote. Hodnoty Rx, Ry, Rz v skutočnosti lineárne súvisia s hodnotami, ktoré bude produkovať váš akcelerometer v reálnom živote a ktoré môžete použiť na vykonávanie rôznych výpočtov.
Než sa tam dostaneme, porozprávajme sa trochu o spôsobe, akým nám tieto informácie akcelerometre poskytnú. Väčšina akcelerometrov bude zaradená do dvoch kategórií: digitálne a analógové. Digitálne akcelerometre vám poskytnú informácie pomocou sériového protokolu, ako napríklad I2C, SPI alebo USART, zatiaľ čo analógové akcelerometre poskytnú výstup napätia v preddefinovanom rozsahu, ktorý musíte previesť na digitálnu hodnotu pomocou modulu ADC (analógovo -digitálny prevodník). Nebudem sa veľmi rozpisovať o tom, ako funguje ADC, jednak preto, že je to taká rozsiahla téma, a jednak preto, že sa líši od jednej platformy k druhej. Niektoré mikrokontroléry budú mať vstavané moduly ADC, niektoré z nich budú potrebovať externé komponenty na vykonávanie konverzií ADC. Bez ohľadu na to, aký typ modulu ADC použijete, skončíte s hodnotou v určitom rozsahu. Napríklad 10 -bitový modul ADC bude produkovať hodnotu v rozsahu 0..1023, všimnite si, že 1023 = 2^10 -1. 12-bitový modul ADC bude produkovať hodnotu v rozsahu 0..4095, všimnite si, že 4095 = 2^12-1.
Poďme ďalej zvážením jednoduchého príkladu, predpokladajme, že náš 10bitový modul ADC nám poskytol nasledujúce hodnoty pre tri kanály (osi) akcelerometra:
AdcRx = 586 AdcRy = 630 AdcRz = 561
Každý modul ADC bude mať referenčné napätie, predpokladajme, že v našom prípade je 3,3V. Na prevod 10bitovej hodnoty adc na napätie použijeme nasledujúci vzorec:
VoltsRx = AdcRx * Vref / 1023
Tu je stručná poznámka: pre 8bitový ADC bude posledný delič 255 = 2 ^ 8 -1 a pre 12bitový ADC bude posledný delič 4095 = 2 ^ 12 -1.
Použitím tohto vzorca na všetky 3 kanály získame:
VoltsRx = 586 * 3,3V / 1023 = ~ 1,89V (všetky výsledky zaokrúhlime na 2 desatinné miesta) VoltsRy = 630 * 3,3V / 1023 = ~ 2,03V VoltsRz = 561 * 3,3V / 1023 = ~ 1,81V
Každý akcelerometer má úroveň napätia nula g, nájdete ho v špecifikáciách, toto je napätie, ktoré zodpovedá 0 g. Aby sme získali podpísanú hodnotu napätia, musíme vypočítať posun z tejto úrovne. Povedzme, že naša úroveň napätia 0g je VzeroG = 1,65V. Posuny napätia z napätia nuly g vypočítame nasledovne:
DeltaVoltsRx = 1,89V - 1,65V = 0,24V DeltaVoltsRy = 2,03V - 1,65V = 0,38V DeltaVoltsRz = 1,81V - 1,65V = 0,16V
Teraz máme namerané hodnoty akcelerometra vo voltoch, stále to nie je v g (9,8 m/s^2), na konečnú konverziu použijeme citlivosť akcelerometra, zvyčajne vyjadrenú v mV/g. Povedzme, že naša citlivosť = 478,5 mV/g = 0,4785 V/g. Hodnoty citlivosti nájdete v špecifikáciách akcelerometra. Na získanie konečných hodnôt síl vyjadrených v g použijeme nasledujúci vzorec:
Rx = DeltaVoltsRx / citlivosť
Rx = 0,24V / 0,4785V / g = ~ 0,5g Ry = 0,38V / 0,4785V / g = ~ 0,79g Rz = 0,16V / 0,4785V / g = ~ 0,33g
Mohli by sme samozrejme skombinovať všetky kroky do jedného vzorca, ale prešiel som všetkými krokmi, aby bolo jasné, ako prejdete od čítania ADC k zložke vektora sily vyjadrenej v g.
Rx = (AdcRx * Vref / 1023 - VzeroG) / Citlivosť (Rov. 2) Ry = (AdcRy * Vref / 1023 - VzeroG) / Citlivosť Rz = (AdcRz * Vref / 1023 - VzeroG) / Citlivosť
Teraz máme všetky 3 zložky, ktoré definujú náš vektor zotrvačnej sily, ak zariadenie nie je vystavené iným silám okrem gravitácie, môžeme predpokladať, že toto je smer nášho vektora gravitačnej sily. Ak chcete vypočítať sklon zariadenia voči zemi, môžete vypočítať uhol medzi týmto vektorom a osou Z. Ak vás zaujíma aj smer sklonu na osu, môžete tento výsledok rozdeliť na 2 zložky: sklon na osi X a Y, ktorý je možné vypočítať ako uhol medzi gravitačným vektorom a osami X / Y. Výpočet týchto uhlov je jednoduchší, ako by ste si mohli myslieť, keď sme teraz vypočítali hodnoty pre Rx, Ry a Rz. Vráťme sa k poslednému modelu akcelerometra a urobíme niekoľko ďalších zápisov:
Úhly, ktoré nás zaujímajú, sú uhly medzi osami X, Y, Z a silovým vektorom R. Tieto uhly definujeme ako Axr, Ayr, Azr. Z pravouhlého trojuholníka tvoreného R a Rx si môžete všimnúť, že:
cos (Axr) = Rx / R a podobne: cos (Ayr) = Ry / R cos (Azr) = Rz / R
Z Rov. 1 môžeme odpočítať, že R = SQRT (Rx^2 + Ry^2 + Rz^2).
Teraz môžeme nájsť svoje uhly pomocou funkcie arccos () (inverzná funkcia cos ()):
Axr = arccos (Rx/R) Ayr = arccos (Ry/R) Azr = arccos (Rz/R)
Prešli sme dlhú cestu k vysvetleniu modelu akcelerometra, len aby sme prišli na tieto vzorce. V závislosti od vašich aplikácií možno budete chcieť použiť akékoľvek prechodné vzorce, ktoré sme odvodili. Čoskoro tiež predstavíme model gyroskopu a uvidíme, ako sa dajú údaje akcelerometra a gyroskopu skombinovať, aby poskytli ešte presnejšie odhady sklonu.
Ale skôr, ako to urobíme, urobme niekoľko užitočných zápisov:
cosX = cos (Axr) = Rx / R útulné = cos (Ayr) = Ry / R cosZ = cos (Azr) = Rz / R
Tento triplet sa často nazýva Smerový kosínus a v zásade predstavuje jednotkový vektor (vektor s dĺžkou 1), ktorý má rovnaký smer ako náš R vektor. Môžete si ľahko overiť, že:
SQRT (cosX^2 + útulný^2 + cosZ^2) = 1
Je to pekná vlastnosť, pretože nás zbavuje monitorovania modulu (dĺžky) R vektora. Ak nás zaujíma smer nášho zotrvačného vektora, často má zmysel normalizovať jeho modul, aby sa zjednodušili ďalšie výpočty.
Krok 2: Gyroskop
Nebudeme predstavovať žiadny ekvivalentný boxový model pre gyroskop, ako sme to urobili pre akcelerometer, namiesto toho skočíme rovno na druhý model akcelerometra a ukážeme si, čo meria gyroskop podľa tohto modelu.
Každý kanál gyroskopu meria rotáciu okolo jednej z osí. Napríklad 2-osý gyroskop bude merať rotáciu okolo osí X a Y (alebo niektorí môžu hovoriť „o“). Aby sme túto rotáciu vyjadrili v číslach, urobme niekoľko zápisov. Najprv definujme:
Rxz - je priemet vektora zotrvačnej sily R na rovinu XZ Ryz - je priemet vektora zotrvačnej sily R na rovinu YZ
Z pravouhlého trojuholníka tvoreného Rxz a Rz pomocou Pythagorovej vety dostaneme:
Rxz^2 = Rx^2 + Rz^2 a podobne: Ryz^2 = Ry^2 + Rz^2
tiež si všimnite, že:
R^2 = Rxz^2 + Ry^2, to možno odvodiť z rovníc 1 a vyššie, alebo to možno odvodiť z pravouhlého trojuholníka tvoreného R a Ryz R^2 = Ryz^2 + Rx^2
V tomto článku nebudeme používať tieto vzorce, ale je užitočné poznamenať si vzťah medzi všetkými hodnotami v našom modeli.
Namiesto toho definujeme uhol medzi osou Z a Rxz, Ryz vektormi nasledovne:
Axz - je uhol medzi Rxz (priemet R na rovinu XZ) a os Z Ayz - je uhol medzi Ryz (priemet R na rovinu YZ) a osou Z
Teraz sa dostávame bližšie k tomu, čo meria gyroskop. Gyroskop meria rýchlosť zmien uhlov definovaných vyššie. Inými slovami, bude produkovať hodnotu, ktorá je lineárne spojená s rýchlosťou zmeny týchto uhlov. Aby sme to vysvetlili, predpokladajme, že sme zmerali uhol natočenia okolo osi Y (to by bol uhol Axz) v čase t0 a definovali sme ho ako Axz0, potom sme tento uhol zmerali v neskoršom čase t1 a bol to Axz1. Rýchlosť zmeny sa vypočíta takto:
RateAxz = (Axz1 - Axz0) / (t1 - t0).
Ak vyjadríme Axz v stupňoch a čas v sekundách, potom bude táto hodnota vyjadrená v deg/s. Práve to meria gyroskop.
V praxi vám gyroskop (pokiaľ nejde o špeciálny digitálny gyroskop) len zriedka poskytne hodnotu vyjadrenú v deg/s. Rovnako ako pre akcelerometer získate hodnotu ADC, ktorú budete musieť previesť na stupne deg/s pomocou vzorca podobného ekv. 2, ktorý sme definovali pre akcelerometer. Predstavme prevodný vzorec ADC na deg/s pre gyroskop (predpokladáme, že používame 10bitový modul ADC, pre 8bitový ADC nahraďte 1023 číslom 255, pre 12bitový ADC nahraďte 1023 číslom 4095).
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Citlivosť Eq.3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / Citlivosť
AdcGyroXZ, AdcGyroYZ - sú získané z nášho modulu adc a predstavujú kanály, ktoré merajú rotáciu projekcie R vektora v XZ, respektíve v rovinách YZ, čo je ekvivalentom tvrdenia, že rotácia bola vykonaná okolo osí Y a X, v uvedenom poradí.
Vref - je referenčné napätie ADC, ktoré použijeme 3,3 V v nižšie uvedenom príklade VzeroRate - je napätie s nulovou rýchlosťou, inými slovami napätie, ktoré gyroskop vydáva, keď nie je predmetom žiadneho otáčania, pre dosku Acc_Gyro je napríklad 1,23 V (tieto hodnoty nájdete v špecifikáciách) Citlivosť - je citlivosť vášho gyroskopu vyjadrená v mV / (deg / s) často zapísaná ako mV / deg / s, v zásade vám hovorí, koľko mV bude výkon gyroskopu sa zvýši, ak zvýšite rýchlosť otáčania o jeden deg/s. Citlivosť dosky Acc_Gyro je napríklad 2 mV/deg/s alebo 0,002 V/deg/s
Vezmime si príklad, predpokladajme, že náš modul ADC vrátil nasledujúce hodnoty:
AdcGyroXZ = 571 AdcGyroXZ = 323
Pomocou vyššie uvedeného vzorca a pomocou parametrov špecifikácií dosky Acc_Gyro získame:
RateAxz = (571 * 3,3V/1023 - 1,23V)/(0,002V/deg/s) = ~ 306 stupňov/s RateAyz = (323 * 3,3V/1023 - 1,23V)/(0,002V/deg/s) = ~ -94 stupňov/s
Inými slovami, zariadenie sa otáča okolo osi Y (alebo môžeme povedať, že sa otáča v rovine XZ) rýchlosťou 306 stupňov/s a okolo osi X (alebo môžeme povedať, že sa otáča v rovine YZ) rýchlosťou - 94 stupňov/s. Upozorňujeme, že znamienko mínus znamená, že sa zariadenie otáča v opačnom smere ako konvenčný kladný smer. Podľa konvencie je jeden smer otáčania kladný. Dobrý list so špecifikáciou pre gyroskop vám ukáže, ktorý smer je kladný, inak ho budete musieť nájsť experimentovaním so zariadením a zistením, ktorý smer otáčania má za následok zvýšenie napätia na výstupnom kolíku. To sa najlepšie robí pomocou osciloskopu, pretože akonáhle zastavíte otáčanie, napätie klesne späť na úroveň nulovej rýchlosti. Ak používate multimetr, musíte udržiavať konštantnú rýchlosť otáčania najmenej niekoľko sekúnd a zaznamenať napätie počas tohto otáčania, potom ho porovnajte s napätím s nulovou rýchlosťou. Ak je napätie vyššie ako napätie s nulovou rýchlosťou, znamená to, že smer otáčania je kladný.
Krok 3: Kombinácia akcelerometra a gyroskopu
Všetko dohromady - kombinácia údajov akcelerometra a gyroskopu
Ak čítate tento článok, pravdepodobne ste získali alebo plánujete získať zariadenie IMU, alebo pravdepodobne plánujete postaviť zariadenie zo samostatných zariadení s akcelerometrom a gyroskopom.
Prvým krokom pri použití kombinovaného zariadenia IMU, ktoré kombinuje akcelerometer a gyroskop, je zosúladenie ich súradnicových systémov. Najjednoduchší spôsob, ako to urobiť, je vybrať súradnicový systém akcelerometra ako referenčný súradnicový systém. Väčšina dátových listov akcelerometra bude zobrazovať smer osí X, Y, Z vzhľadom na obraz fyzického čipu alebo zariadenia. Tu sú napríklad smery osí X, Y, Z, ako sú uvedené v špecifikáciách pre dosku Acc_Gyro:
Ďalšie kroky sú:
Identifikujte výstupy gyroskopu, ktoré zodpovedajú hodnotám RateAxz, RateAyz diskutovaným vyššie. Zistite, či je potrebné tieto výstupy invertovať kvôli fyzickej polohe gyroskopu vzhľadom na akcelerometer
Nepredpokladajte, že ak má gyroskop výstup označený X alebo Y, bude zodpovedať akejkoľvek osi súradnicového systému akcelerometra, aj keď je tento výstup súčasťou jednotky IMU. Najlepším spôsobom je otestovať to. Za predpokladu, že ste fixovali polohu gyroskopu vzhľadom na akcelerometer. Predpokladá sa, že okraje gyroskopu a akcelerometra sú navzájom rovnobežné, to znamená, že gyroskop umiestnite v uhle násobku 90 stupňov voči čipu akcelerometra. Ak ste získali dosku IMU, je pravdepodobné, že sú už zarovnané týmto spôsobom. V tomto článku nebudeme diskutovať o modeloch, kde je gyroskop umiestnený v nepravidelnom uhle vzhľadom na akcelerometer (povedzme 45 alebo 30 stupňov), aj keď to môže byť v niektorých aplikáciách užitočné.
Tu je ukážková sekvencia na určenie, ktorý výstup gyroskopu zodpovedá vyššie uvedenej hodnote RateAxz.
- začnite umiestnením zariadenia do vodorovnej polohy. Výstupy akcelerometra X aj Y by vydali napätie nula g (napríklad pre dosku Acc_Gyro je to 1,65 V)
- nabudúce začnite otáčať zariadením okolo osi Y, inak to môžete povedať tak, že zariadenie otočíte v rovine XZ, aby sa výstupy akcelerometra X a Z menili a výstup Y zostal konštantný. - pri otáčaní zariadenia konštantnou rýchlosťou, ktorý výstup gyroskopu sa mení, by ostatné výstupy gyroskopu mali zostať konštantné - výstup gyroskopu, ktorý sa zmenil počas otáčania okolo osi Y (otáčanie v rovine XZ), poskytne vstupnú hodnotu pre AdcGyroXZ, z ktorého vypočítame RateAxz - posledným krokom je zaistiť, aby smer otáčania zodpovedal nášmu modelu, v niektorých prípadoch možno budete musieť obrátiť hodnotu RateAxz kvôli fyzickej polohe gyroskopu vzhľadom na akcelerometer - znova vykonajte vyššie uvedený test a zariadenie otáčajte os Y, tentokrát monitorujte výstup X akcelerometra (v našom modeli AdcRx). Ak AdcRx rastie (prvých 90 stupňov rotácie z horizontálnej polohy), potom by mal rásť aj AdcGyroXZ. V opačnom prípade musíte invertovať RateAxz, môžete to dosiahnuť zavedením znamienka do Eq.3 nasledovne:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / Citlivosť, kde InvertAxz je 1 alebo -1
pre RateAyz urobte rovnakú testovaciu skúšku, otáčaním zariadenia okolo osi X môžete zistiť, ktorý výstup gyroskopu zodpovedá RateAyz a či je potrebné ho prevrátiť. Keď získate hodnotu pre InvertAyz, mali by ste na výpočet RateAyz použiť nasledujúci vzorec:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / Citlivosť
Ak by ste urobili tieto testy na doske Acc_Gyro, získali by ste nasledujúce výsledky:
- výstupný pin pre RateAxz je GX4 a InvertAxz = -1. - výstupný pin pre RateAyz je GY4 a InvertAyz = -1
Od tohto bodu budeme uvažovať o tom, že ste svoju IMU nastavili tak, aby ste mohli vypočítať správne hodnoty pre Axr, Ayr, Azr (podľa definície v časti 1. Akcelerometer) a RateAxz, RateAyz (podľa definície v časti 2. Gyroskop)). Ďalej budeme analyzovať vzťahy medzi týmito hodnotami, ktoré sa ukázali byť užitočné pri získavaní presnejších odhadov sklonu zariadenia voči základnej rovine.
V tomto bode si možno kladiete otázku, ak nám model akcelerometra už poskytol uhly sklonu Axr, Ayr, Azr, prečo by sme sa chceli obťažovať údajmi gyroskopu? Odpoveď je jednoduchá: dátam akcelerometra nemožno vždy stopercentne dôverovať. Existuje niekoľko dôvodov, pamätajte na to, že akcelerometer meria zotrvačnú silu, taká sila môže byť spôsobená gravitáciou (a ideálne iba gravitáciou), ale môže to byť tiež spôsobené zrýchlením (pohybom) zariadenia. Výsledkom je, že aj keď je akcelerometer v relatívne stabilnom stave, je stále veľmi citlivý na vibrácie a mechanický hluk všeobecne. To je hlavný dôvod, prečo väčšina systémov IMU používa na vyhladenie chýb akcelerometra gyroskop. Ale ako sa to robí? A je gyroskop bez šumu?
Gyroskop nie je bez šumu, pretože meria rotáciu, je menej citlivý na lineárne mechanické pohyby, na typ hluku, ktorým trpí akcelerometer, ale gyroskopy majú iné typy problémov, ako napríklad drift (nevrátenie sa na hodnotu nulovej rýchlosti) keď sa otáčanie zastaví). Napriek tomu spriemerovaním údajov pochádzajúcich z akcelerometra a gyroskopu môžeme získať relatívne lepší odhad aktuálneho sklonu zariadenia, než by sme získali použitím samotných dát akcelerometra.
V ďalších krokoch predstavím algoritmus, ktorý bol inšpirovaný niektorými myšlienkami použitými v Kalmanovom filtri, je však oveľa jednoduchšie a jednoduchšie ho implementovať na vstavaných zariadeniach. Predtým sa najskôr pozrime, čo chceme, aby náš algoritmus vypočítal. Je to práve smer vektora gravitačnej sily R = [Rx, Ry, Rz], z ktorého môžeme odvodiť ďalšie hodnoty ako Axr, Ayr, Azr alebo cosX, útulný, cosZ, ktorý nám poskytne predstavu o sklone nášho zariadenia. vzhľadom na základnú rovinu diskutujeme o vzťahu medzi týmito hodnotami v časti 1. Dalo by sa povedať - nemáme už tieto hodnoty Rx, Ry, Rz z rovnice 2 v časti 1? Áno, ale pamätajte na to, že tieto hodnoty sú odvodené iba z údajov akcelerometra, takže ak by ste ich chceli použiť priamo vo svojej aplikácii, môžete zaznamenať viac hluku, ako môže vaša aplikácia tolerovať. Aby sme sa vyhli ďalším nedorozumeniam, nanovo definujeme merania akcelerometra nasledovne:
Racc - je vektor zotrvačnej sily meraný akcelerometrom, ktorý pozostáva z nasledujúcich komponentov (projekcie na osi X, Y, Z):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / Sensitivity RyAcc = (AdcRy * Vref / 1023 - VzeroG) / Sensitivity RzAcc = (AdcRz * Vref / 1023 - VzeroG) / Sensitivity
Zatiaľ máme súbor nameraných hodnôt, ktoré môžeme získať čisto z hodnôt ADC akcelerometra. Tento súbor údajov budeme nazývať „vektor“a použijeme nasledujúci zápis.
Racc = [RxAcc, RyAcc, RzAcc]
Pretože tieto komponenty Racc je možné získať z údajov akcelerometra, môžeme to považovať za vstup do nášho algoritmu.
Upozorňujeme, že pretože Racc meria gravitačnú silu, budete mať pravdu, ak predpokladáte, že dĺžka tohto vektora definovaného nižšie je rovnaká alebo blízka 1 g.
| Racc | = SQRT (RxAcc^2 + RyAcc^2 + RzAcc^2), Aby ste si boli istí, že má zmysel aktualizovať tento vektor nasledovne:
Racc (normalizované) = [RxAcc/| Racc |, RyAcc/| Racc |, RzAcc/| Racc |].
Tým sa zabezpečí, že dĺžka vášho normalizovaného Racc vektora je vždy 1.
Ďalej predstavíme nový vektor a nazveme ho
Odpočinok = [RxEst, RyEst, RzEst]
Toto bude výstup z nášho algoritmu, jedná sa o opravené hodnoty na základe údajov gyroskopu a na základe predchádzajúcich odhadovaných údajov.
Tu je postup, ktorý náš algoritmus urobí: - akcelerometer nám hovorí: „Teraz ste na pozícii Racc“- hovoríme „Ďakujem, ale dovoľte mi skontrolovať“, - potom opravte tieto informácie pomocou údajov gyroskopu, ako aj s údajmi z minulosti a vydáme nový odhadovaný vektorový zvyšok. - Rest považujeme za našu „najlepšiu stávku“, pokiaľ ide o aktuálnu polohu zariadenia.
Pozrime sa, ako to dokážeme dosiahnuť.
Našu postupnosť začneme dôverou nášmu akcelerometru a priradením:
Zvyšok (0) = Racc (0)
Mimochodom, Rest a Racc sú vektory, takže vyššie uvedená rovnica je len jednoduchý spôsob, ako napísať 3 sady rovníc a vyhnúť sa opakovaniu:
RxEst (0) = RxAcc (0) RyEst (0) = RyAcc (0) RzEst (0) = RzAcc (0)
Ďalej budeme vykonávať pravidelné merania v rovnakých časových intervaloch T sekúnd a získame nové merania, ktoré definujeme ako Racc (1), Racc (2), Racc (3) a tak ďalej. Tiež vydáme nové odhady v každom časovom intervale Odpočinok (1), Odpočinok (2), Odpočinok (3) atď.
Predpokladajme, že sme v kroku n. Máme dve známe sady hodnôt, ktoré by sme chceli použiť:
Zvyšok (n -1) - náš predchádzajúci odhad, pričom zvyšok (0) = Racc (0) Racc (n) - naše aktuálne meranie akcelerometra
Predtým, ako budeme môcť vypočítať zvyšok (n), predstavme si novú nameranú hodnotu, ktorú môžeme získať z nášho gyroskopu a predchádzajúceho odhadu.
Hovoríme mu Rgyro a je to tiež vektor pozostávajúci z 3 zložiek:
Rgyro = [RxGyro, RyGyro, RzGyro]
Tento vektor vypočítame po jednej zložke. Začneme RxGyro.
Začnime pozorovaním nasledujúceho vzťahu v našom modeli gyroskopu, z pravouhlého trojuholníka tvoreného Rz a Rxz môžeme odvodiť, že:
tan (Axz) = Rx/Rz => Axz = atan2 (Rx, Rz)
Atan2 môže byť funkcia, ktorú ste nikdy predtým nepoužili, je podobná atan, ibaže vracia hodnoty v rozsahu (-PI, PI) na rozdiel od (-PI/2, PI/2) ako vráti atan a trvá 2 argumenty namiesto jedného. Umožňuje nám previesť dve hodnoty Rx, Rz na uhly v celom rozsahu 360 stupňov (-PI na PI). Viac o atan2 si môžete prečítať tu.
Keď teda poznáme RxEst (n-1) a RzEst (n-1), môžeme nájsť:
Axz (n-1) = atan2 (RxEst (n-1), RzEst (n-1)).
Nezabudnite, že gyroskop meria rýchlosť zmeny uhla Axz. Nový uhol Axz (n) teda môžeme odhadnúť nasledovne:
Axz (n) = Axz (n-1) + RateAxz (n) * T
Nezabudnite, že RateAxz je možné získať z nameraných hodnôt gyroskopu ADC. Presnejší vzorec môže používať priemernú rýchlosť otáčania vypočítanú nasledovne:
RateAxzAvg = (RateAxz (n) + RateAxz (n-1)) / 2 Axz (n) = Axz (n-1) + RateAxzAvg * T
Rovnakým spôsobom môžeme nájsť:
Ayz (n) = Ayz (n-1) + sadzbaAyz (n) * T
Ok, takže teraz máme Axz (n) a Ayz (n). Odkiaľ pôjdeme odtiaľto, aby sme odpočítali RxGyro/RyGyro? Z rov. 1, môžeme napísať dĺžku vektora Rgyro nasledovne:
| Rgyro | = SQRT (RxGyro^2 + RyGyro^2 + RzGyro^2)
Tiež pretože sme normalizovali náš Racc vektor, môžeme predpokladať, že jeho dĺžka je 1 a po otočení sa nezmenil, takže je relatívne bezpečné písať:
| Rgyro | = 1
Prijmime dočasný kratší zápis pre nižšie uvedené výpočty:
x = RxGyro, y = RyGyro, z = RzGyro
Pomocou vyššie uvedených vzťahov môžeme napísať:
x = x / 1 = x / SQRT (x^2+y^2+z^2)
Rozdeľme čitateľa a menovateľa zlomku na SQRT (x^2 + z^2)
x = (x / SQRT (x^2 + z^2)) / SQRT ((x^2 + y^2 + z^2) / (x^2 + z^2))
Všimnite si, že x / SQRT (x^2 + z^2) = sin (Axz), takže:
x = sin (Axz) / SQRT (1 + y^2 / (x^2 + z^2))
Teraz vynásobte čitateľa a menovateľa zlomku v SQRT z^2
x = sin (Axz) / SQRT (1 + y^2 * z^2 / (z^2 * (x^2 + z^2)))
Všimnite si toho, že z / SQRT (x^2 + z^2) = cos (Axz) a y / z = tan (Ayz), takže nakoniec:
x = sin (Axz) / SQRT (1 + cos (Axz)^2 * tan (Ayz)^2)
Keď sa vrátime k nášmu zápisu, dostaneme:
RxGyro = sin (Axz (n)) / SQRT (1 + cos (Axz (n))^2 * tan (Ayz (n))^2)
rovnakým spôsobom to zistíme
RyGyro = sin (Ayz (n)) / SQRT (1 + cos (Ayz (n))^2 * tan (Axz (n))^2)
Teraz konečne môžeme nájsť:
RzGyro = Znamenie (RzGyro)*SQRT (1 - RxGyro^2 - RyGyro^2).
Kde Znak (RzGyro) = 1, keď RzGyro> = 0, a Znak (RzGyro) = -1, keď RzGyro <0.
Jeden jednoduchý spôsob, ako to odhadnúť, je vziať si:
Znak (RzGyro) = Znak (RzEst (n-1))
V praxi dávajte pozor, keď sa RzEst (n-1) blíži k 0. V tomto prípade môžete gyroskopickú fázu úplne vynechať a priradiť: Rgyro = Odpočinok (n-1). Rz sa používa ako referencia na výpočet uhlov Axz a Ayz a keď je blízko 0, hodnoty môžu pretekať a spôsobiť zlé výsledky. Budete v doméne veľkých čísel s pohyblivou rádovou čiarkou, kde implementáciám funkcií tan () / atan () môže chýbať presnosť.
Zrekapitulujme si teda, čo zatiaľ máme, sme v kroku n nášho algoritmu a vypočítali sme nasledujúce hodnoty:
Racc - údaje o prúde z nášho akcelerometra Rgyro - získané z odpočtu (n -1) a odčítania aktuálneho gyroskopu
Aké hodnoty používame na výpočet aktualizovaného odhadu Rest (n)? Pravdepodobne ste uhádli, že použijeme oboje. Použijeme vážený priemer, aby:
Zvyšok (n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
Tento vzorec môžeme zjednodušiť vydelením čitateľa a menovateľa zlomku w1.
Zvyšok (n) = (Racc * w1/w1 + Rgyro * w2/w1)/(w1/w1 + w2/w1)
a po nahradení w2/w1 = wGyro dostaneme:
Zvyšok (n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
Vo vyššie uvedenom fóre nám wGyro hovorí, do akej miery veríme svojmu gyroskopu v porovnaní s naším akcelerometrom. Túto hodnotu je možné zvoliť experimentálne, dobré výsledky zvyčajne dosiahnu hodnoty medzi 5..20.
Hlavný rozdiel tohto algoritmu od Kalmanovho filtra je v tom, že táto hmotnosť je relatívne pevná, zatiaľ čo v Kalmanovom filtri sú hmotnosti trvalo aktualizované na základe nameraného hluku nameraných hodnôt akcelerometra. Kalmanov filter je zameraný na to, aby vám poskytol „najlepšie“teoretické výsledky, zatiaľ čo tento algoritmus vám môže poskytnúť výsledky „dostatočne dobré“na praktické využitie. Môžete implementovať algoritmus, ktorý upravuje wGyro v závislosti od niektorých faktorov hluku, ktoré meriate, ale pevné hodnoty budú fungovať dobre pre väčšinu aplikácií.
Sme krok od získania našich aktualizovaných odhadovaných hodnôt:
RxEst (n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst (n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst (n) = (RzAcc + RzGyro * wGyro) / (1 + w Gyro)
Teraz normalizujme tento vektor znova:
R = SQRT (RxEst (n)^2 + RyEst (n)^2 + RzEst (n)^2)
RxEst (n) = RxEst (n)/R RyEst (n) = RyEst (n)/R RzEst (n) = RzEst (n)/R
A sme pripravení znova zopakovať svoju slučku.
Tento sprievodca sa pôvodne objavil na starlino.com, urobil som niekoľko ľahkých úprav a so súhlasom som ho znova uverejnil. Ďakujem Starlino!
Odporúča:
Gyroskop MPU 6050, akcelerometer, komunikácia s Arduino (Atmega328p): 5 krokov
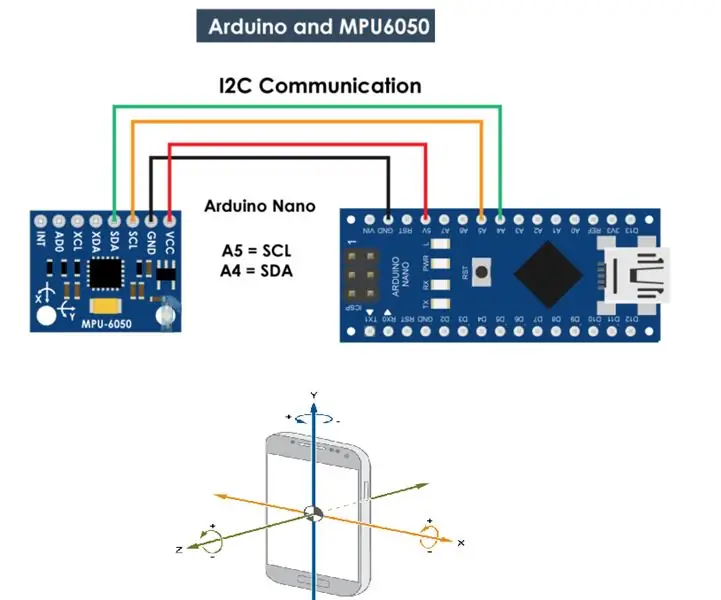
Gyroskop MPU 6050, akcelerometer s Arduino (Atmega328p): MPU6050 IMU má v jednom čipe integrovaný trojosový akcelerometer aj trojosový gyroskop. Gyroskop meria rýchlosť otáčania alebo rýchlosť zmeny uhlovej polohy v priebehu času pozdĺž Os X, Y a Z. Výstupy gyroskopu sú
Raspberry Pi - 3 -osý akcelerometer ADXL345 Java, návod: 4 kroky

Raspberry Pi-3-osový akcelerometer ADXL345 Java Výukový program: ADXL345 je malý, tenký, ultra nízky výkon, 3-osový akcelerometer s meraním s vysokým rozlíšením (13 bitov) až ± 16 g. Digitálne výstupné údaje sú formátované ako 16-bitové dvojčatá a sú prístupné prostredníctvom digitálneho rozhrania I2 C. Meria
Návod na akcelerometer CubeSat: 6 krokov

CubeSat Accelerometer Tutorial: Cubesat je typ miniaturizovanej družice pre vesmírny výskum, ktorý sa skladá z násobkov kubických jednotiek 10x10x10 cm a hmotnosti najviac 1,33 kilogramu na jednotku. Cubesats umožňuje odoslanie veľkého množstva satelitov do vesmíru a
3-osový 12-bitový/8-bitový digitálny akcelerometer Raspberry Pi MMA8452Q Java návod: 4 kroky

Trojosový 12-bitový/8-bitový digitálny akcelerometer Raspberry Pi MMA8452Q Java: MMA8452Q je inteligentný, trojosový, kapacitný, mikroobrábaný akcelerometer s nízkym výkonom a 12 bitovým rozlíšením. Flexibilné programovateľné možnosti pre používateľov sú k dispozícii pomocou vstavaných funkcií v akcelerometri, konfigurovateľných na dve prerušenia
Trojosový akceleračný gyroskop GY-521 MPU6050, modul 6DOF, návod: 4 kroky

Trojosový akceleračný gyroskop GY-521 MPU6050 6DOF Modul Výukový program: Popis Tento jednoduchý modul obsahuje všetko potrebné na prepojenie s Arduino a inými ovládačmi cez I2C (použite knižnicu Wire Arduino) a poskytuje informácie o snímaní pohybu pre 3 osi-X, Y a Z .SpecifikáciaRozsah akcelerometra: ± 2, ±
